
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;并估计,以运动为主的休闲方式的人的比例;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2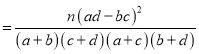 .
.
科目:高中数学 来源: 题型:
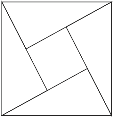
【题目】2002年8月在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,设直角三角形中较小的锐角为![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() .若
.若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
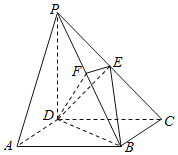
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的营销部门对某件商品在网上销售情况进行调查,发现当这件商品每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到以下表:
![]()
(1)经分析发现,可用线性回归模型拟合该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)该公司为了在购物节期间对所有商品价格进行新一轮调整,随机抽查了上一年购物节期间60名网友的网购金额情况,得到如下数据统计表:
网购金额 (单位:千元) |
|
|
|
|
|
| 合计 |
频数 | 3 | 9 | 9 | 15 | 18 | 6 | 60 |
若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”.该营销部门为了进步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设![]() 为选取的3人中“网购达人”的人数,求
为选取的3人中“网购达人”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:①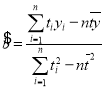 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
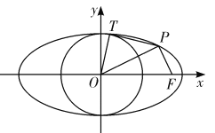
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.
(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com