
分析 (1)利用直角坐标方程化为极坐标方程的方法,求圆C的极坐标方程;
(2)利用|MN|=|ρ1-ρ2|,求线段MN的长.
解答 解:(1)(x-$\sqrt{3}$)2+(y+1)2=9可化为x2+y2-2$\sqrt{3}$x+2y-5=0,
故其极坐标方程为ρ2-2$\sqrt{3}$ρcosθ+2ρsinθ-5=0.…(5分)
(2)将θ=$\frac{π}{6}$代入ρ2-2$\sqrt{3}$ρcosθ+2ρsinθ-5=0,得ρ2-2ρ-5=0,
∴ρ1+ρ2=2,ρ1ρ2=-5,
∴|MN|=|ρ1-ρ2|=$\sqrt{4+20}$=2$\sqrt{6}$.…(10分)
点评 本题主要考查把直角坐标方程化为极坐标方程的方法,求两曲线的位置关系,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=lg10x | C. | y=($\sqrt{x}$)2 | D. | y=10lgx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+$\frac{y}{3}$=1 | B. | $\frac{x}{6}$+$\frac{y}{2}$=1 | C. | $\frac{x}{4}$+$\frac{y}{4}$=1 | D. | $\frac{x}{12}$+$\frac{3y}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
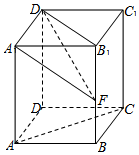 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为$\sqrt{2}$的正方形,AA1=3,点F在棱B1B上运动.
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为$\sqrt{2}$的正方形,AA1=3,点F在棱B1B上运动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | ab>1 | D. | lg(b-a)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ | D. | $y=\sqrt{x}+\frac{4}{{\sqrt{x}}}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com