
分析 随机变量X~B(20,$\frac{1}{2}$),当P(X=k)=${C}_{20}^{k}•(\frac{1}{2})^{20}$,由式子的意义知:概率最大也就是X最可能的取值.这和期望的意义接近.由EX=20×$\frac{1}{2}$=10,k=10是极值,由此能求出P(X=k)取最大值时k的值.
解答 解:∵随机变量X~B(20,$\frac{1}{2}$),
∴当P(X=k)=${C}_{20}^{k}•(\frac{1}{2})^{20}$,
由式子的意义知:概率最大也就是X最可能的取值.这和期望的意义接近.
∵EX=20×$\frac{1}{2}$=10,
∴k=10是极值,
∴P(X=k)取最大值时k的值是10.
故答案为10.
点评 本题考查二项分布的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{{\sqrt{2}}}{2}}]$ | B. | $[{\frac{{\sqrt{2}}}{2},1})$ | C. | $[{0,\frac{{\sqrt{6}}}{3}}]$ | D. | $[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{6}}}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,$\frac{1}{3}$] | C. | [$\frac{1}{3}$,1) | D. | [$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
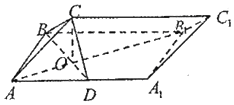 如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1
如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com