
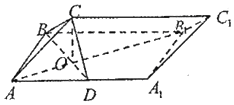
 如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1
如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1分析 (Ⅰ)由$\frac{AB}{AD}$=$\frac{B{B}_{1}}{AB}$=$\sqrt{2}$,可知:Rt△BAD∽Rt△ABB1,可得出BD⊥AB1,根据CO⊥平面ABB1A1得出CO⊥AB1,于是AB1⊥平面BCD,从而得出CD⊥AB1;
(Ⅱ)由题意可知:CO⊥平面AOB,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求得平面ADC的法向量为n,求得$\overrightarrow{BC}$,利用向量的夹角公式,即可得出结论.
解答 解:(Ⅰ)证明:由已知得,$\frac{AB}{AD}$=$\frac{B{B}_{1}}{AB}$=$\sqrt{2}$,
∴Rt△BAD∽Rt△ABB1
∴∠BDA=∠B1AB,∴∠ABD+∠B1AB=∠ABD+∠BDA=90°
∴在△AOB中,∠AOB=180°-(∠ABO+∠OAB )=90°,即BD⊥AB1…4分
另BC⊥AB1,BD∩BC=B,
∴AB1⊥平面BCD,CD?平面BCD,
∴CD⊥AB1 …6分
(Ⅱ) 在Rt△ABD中,AB=1,AD=$\frac{\sqrt{2}}{2}$,
∴AO=$\frac{\sqrt{3}}{3}$
在Rt△AOB中,得BO=$\frac{\sqrt{6}}{3}$,
∴BO2+CO2=BC2,即BO⊥CO,
∴CO⊥平面AOB----8分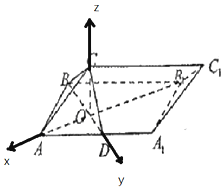
建立如图坐标系,设BC与平面ACD所成的角为θ,
∵$A(\frac{{\sqrt{3}}}{3},0,0),B(0,-\frac{{\sqrt{6}}}{3},0),C(0,0,\frac{{\sqrt{3}}}{3}),D(0,\frac{{\sqrt{3}}}{3},0)$,
设平面ADC的法向量为n.解得n=(1,1,1).
$\overrightarrow{BC}=({0,\frac{{\sqrt{6}}}{3},\frac{{\sqrt{3}}}{3}})$,
∴$sinθ=\frac{{\overrightarrow n•\overrightarrow{BC}}}{{|{\overrightarrow n}||{\overrightarrow{BC}}|}}=\frac{{\sqrt{2}+1}}{3}$,
即BC与平面ACD所成角的正弦值为$\frac{{\sqrt{2}+1}}{3}$.12分.
点评 本题考查了线面垂直的判定与性质,空间向量的应用与线面角的夹角公式,考查向量方法的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
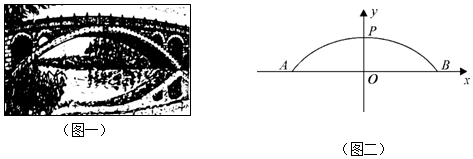
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
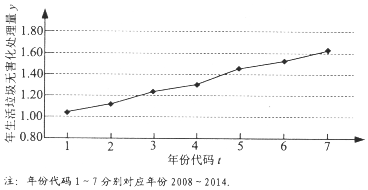
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63或126 | B. | 252 | C. | 120 | D. | 63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com