
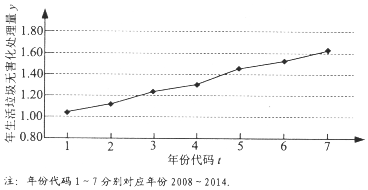
分析 (Ⅰ)由折线图看出,y与t之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;
(Ⅱ)根据已知中的数据,求出回归系数,可得回归方程,2016年对应的t值为9,代入可预测2016年我国生活垃圾无害化处理量.
解答 解:(Ⅰ)由折线图看出,y与t之间存在较强的正相关关系,理由如下:
∵r=$\frac{40.17-4×9.32}{2\sqrt{7}×0.55}$≈0.993,
∵0.993>0.75,
故y与t之间存在较强的正相关关系;(6分)
(Ⅱ)由$\overline{y}$=$\frac{9.32}{7}$≈1.331及(Ⅰ)得$\stackrel{∧}{b}$=$\frac{2.89}{28}$≈0.103,(8分)
$\stackrel{∧}{a}$=1,331-0.103×4≈0.92.(9分)
∴y关于t的回归方程$\stackrel{∧}{y}$=0.10t+0.92,
2016年对应的t值为9,故$\stackrel{∧}{y}$=0.10×9+0.92=1.82,
预测2016年我国生活垃圾无害化处理量为1.82亿吨.(12分)
点评 本题考查的知识点是线性回归方程,回归分析,计算量比较大,计算时要细心.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:解答题
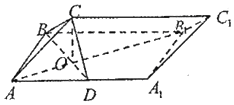 如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1
如图,在三棱柱ABC-A1B1C1中,面ABB1A1为矩形,AB=BC=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,BC⊥AB1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 小于1 | B. | 等于1 | C. | 大于1 | D. | 由b的符号确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com