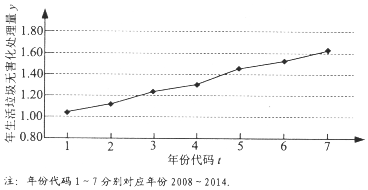
5．如图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图
（I）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；
（II）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量．
参考数据：$\sum_{i=1}^{7}$y
i=9.32，$\sum_{i=1}^{7}$t
iy
i=40.17，$\sqrt{\sum_{i=1}^{7}（{y}_{i}-\overline{y}）^{2}}$=0.55，$\sqrt{7}$≈2.646．
参考公式：相关系数r=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}\sum_{i=1}^{n}（{y}_{u}-\overline{y}）^{2}}}$，$\sum_{i=1}^{n}$（t
i-$\overline{t}$）（y
i-$\overline{y}$）=$\sum_{i=1}^{n}$t
iy
i-$\overline{y}$•$\sum_{i=1}^{n}$t
i-$\overline{t}$•$\sum_{i=1}^{n}$y
i+n$\overline{t}$•$\overline{y}$．
回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$t 中斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{u}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{t}$．
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
