
分析 (1)依题意,求得M坐标,由kAB=kOM,求得b=c,a=$\sqrt{{b}^{2}+{c}^{2}}$,由椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(2)当点Q与椭圆长轴的端点重合时,∠F1QF2的大小为零;当点Q不与椭圆长轴的端点重合时,设∠F1QF2的大小为θ,在△F1QF2中,利用余弦定理,结合基本不等式和椭圆的定义,cos θ═$\frac{2{b}^{2}}{{r}_{1}{r}_{2}}$-1≥$\frac{2{b}^{2}}{(\frac{{r}_{1}+{r}_{2}}{2})^{2}}$-1=0,得到θ∈[0,$\frac{π}{2}$],即为∠F1QF2的取值范围.
解答 解:(1)依题意,作图如图:
设F1(-c,0),则xM=-c,yM=$\frac{{b}^{2}}{a}$,
∴kOM=-$\frac{{b}^{2}}{ac}$,
∵kAB=-$\frac{b}{a}$,∵向量$\overrightarrow{AB}$与$\overrightarrow{OM}$共线,
∴-$\frac{{b}^{2}}{ac}$=-$\frac{b}{a}$,
∴b=c,
由a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$;
(2)设|F1Q|=r1,|F2Q|=r2,∠F1QF2=θ,
∴r1+r2=2a,|F1F2|=2c.
由余弦定理可知:cos θ=$\frac{{r}_{1}^{2}+{r}_{2}^{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$=$\frac{({r}_{1}+{r}_{2})^{2}-2{r}_{1}{r}_{2}-4{c}^{2}}{2{r}_{1}{r}_{2}}$,
=$\frac{2{b}^{2}}{{r}_{1}{r}_{2}}$-1≥$\frac{2{b}^{2}}{(\frac{{r}_{1}+{r}_{2}}{2})^{2}}$-1=$\frac{2{b}^{2}}{{a}^{2}}$-1=0,
当且仅当r1=r2时,cos θ=0,
∴θ∈[0,$\frac{π}{2}$].
点评 本题考查椭圆的标准方程及简单性质,考查向量共线定理,斜率公式,余弦定理及基本不等式的综合应用,考查计算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二象限的角是钝角 | B. | 第三象限的角必大于第二象限的角 | ||
| C. | 方程$sinx-cosx=\frac{1}{2}$无解 | D. | 方程sinx+cosx=2无解 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=$\root{3}{{x}^{3}}$ | C. | f(x)=($\sqrt{x}$)2 | D. | f(x)=$\frac{{x}^{2}}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
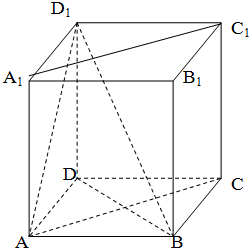 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=$\sqrt{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com