
分析 (Ⅰ)依题意,可得$sinϕ=-\frac{1}{2}$,又$-\frac{π}{2}<ϕ<0$,从而可求ϕ的值;
(Ⅱ)由(Ⅰ)得 $f(x)=2sin(2x-\frac{π}{6})+1$,利用正弦函数的有界性可求函数f(x)的最大值,及取最大值时x的值.
解答 解:(Ⅰ) 因为函数f(x)=2sin(2x+ϕ)+1的图象过点(0,0),
所以 $sinϕ=-\frac{1}{2}$,又$-\frac{π}{2}<ϕ<0$,所以$ϕ=-\frac{π}{6}$.
(Ⅱ)由(Ⅰ)得 $f(x)=2sin(2x-\frac{π}{6})+1$,所以 f(x)max=3,
此时由$2x-\frac{π}{6}=2kπ+\frac{π}{2},得x=kπ+\frac{2π}{3}\;(k∈Z)$.
点评 本题考查正弦函数的图象与性质,求得f(x)=2sin(2x-$\frac{π}{6}$)+1是关键,属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 63或126 | B. | 252 | C. | 120 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
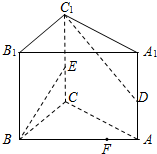 已知直三棱柱ABC-A1B1C1中,D,E分别为AA1,CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.
已知直三棱柱ABC-A1B1C1中,D,E分别为AA1,CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
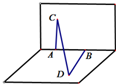 如图,在直二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则直线AB与CD所成角的余弦值为( )
如图,在直二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则直线AB与CD所成角的余弦值为( )| A. | $\frac{{2\sqrt{29}}}{29}$ | B. | $\frac{{\sqrt{29}}}{29}$ | C. | $\frac{{5\sqrt{29}}}{29}$ | D. | $\frac{{2\sqrt{203}}}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\frac{1}{2}$ | B. | $\sqrt{2}-\frac{1}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com