
分析 (Ⅰ)利用二倍角公式以及两角和的正弦函数化简函数的解析式为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期;
(Ⅱ)利用正弦函数的最值求解函数f(x)的最大值及f(x)取最大值时x的集合;
(Ⅲ)利用正弦函数的和单调增区间求解函数f(x)单调递增区间.
解答 解:函数$f(x)={(cosx+sinx)^2}-2sinxcos(\frac{π}{2}-x)$=cos2x+2sinxcosx=cos2x+sin2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)
(Ⅰ)函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(Ⅱ)因为$\sqrt{2}$sin(2x+$\frac{π}{4}$)$≤\sqrt{2}$,
函数f(x)的最大值$\sqrt{2}$,当2x+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z,即x=kπ$+\frac{π}{8}$时,f(x)取最大值,
此时x的集合:{x|x=kπ$+\frac{π}{8}$,k∈Z};
(Ⅲ)2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,k∈Z,
解得$kπ-\frac{3π}{8}$≤x≤kπ$+\frac{π}{8}$,
函数f(x)单调递增区间[$kπ-\frac{3π}{8}$,kπ$+\frac{π}{8}$].k∈Z.
点评 本题考查正弦函数的单调性以及函数的周期性,三角函数的最值的求法,两角和与差的三角函数,考查计算能力.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③④ | B. | ②③④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
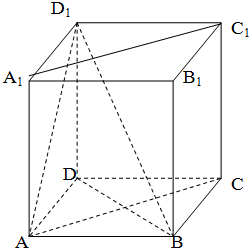 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=$\sqrt{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com