
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{2}$ |
分析 根据函数y=Asin(ωx+φ)的图象变换规律,可得所得图象对应的函数解析式为y=sin(2x+$\frac{π}{4}$-2φ),再根据所得图象关于y轴对称可得$\frac{π}{4}$-2φ=kπ+$\frac{π}{2}$,k∈z,由此求得φ的最小正值.
解答 解:将函数f(x)=sin(2x+$\frac{π}{4}$)的图象向右平移φ个单位,
所得图象对应的函数解析式为y=sin[2(x-φ)+$\frac{π}{4}$]=sin(2x+$\frac{π}{4}$-2φ)关于y轴对称,
则 $\frac{π}{4}$-2φ=kπ+$\frac{π}{2}$,k∈z,即 φ=-$\frac{kπ}{2}$-$\frac{π}{8}$,
故φ的最小正值为$\frac{3π}{8}$,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象的对称性,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 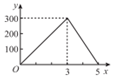 | B. | 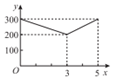 | C. | 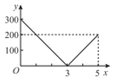 | D. | 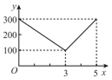 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
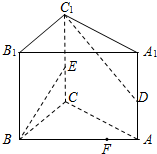 已知直三棱柱ABC-A1B1C1中,D,E分别为AA1,CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.
已知直三棱柱ABC-A1B1C1中,D,E分别为AA1,CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
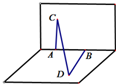 如图,在直二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则直线AB与CD所成角的余弦值为( )
如图,在直二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则直线AB与CD所成角的余弦值为( )| A. | $\frac{{2\sqrt{29}}}{29}$ | B. | $\frac{{\sqrt{29}}}{29}$ | C. | $\frac{{5\sqrt{29}}}{29}$ | D. | $\frac{{2\sqrt{203}}}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | -1003 | D. | 1003 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若$\overrightarrow a•\overrightarrow b=0$,则$\overrightarrow a⊥\overrightarrow b$”的否命题是“若$\overrightarrow a•\overrightarrow b≠0$,则$\overrightarrow a⊥\overrightarrow b$” | |
| B. | 命题“对?x∈R,恒有x2+1>0”的否定是“?x0∈R,使得$x_0^2+1≤0$” | |
| C. | ?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数 | |
| D. | 设p,q是简单命题,若p∨q是真命题,则p∧q也是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com