
如图,在正方体 中,
中,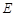 ,
,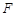 ,
,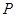 ,
,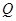 ,
, ,
,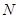 分别是棱
分别是棱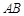 ,
,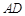 ,
, ,
, 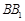 ,
,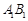 ,
,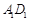 的中点.求证:
的中点.求证:
(1)直线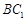 ∥平面
∥平面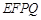 ;
;
(2)直线 ⊥平面
⊥平面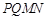 .
.
科目:高中数学 来源: 题型:解答题
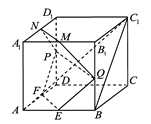
如图,三棱柱 的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。
的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。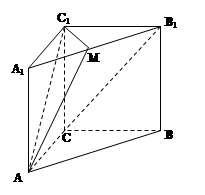

(I)求证:B1C//平面AC1M;
(II)求证:平面AC1M⊥平面AA1B1B.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(1)求证:EF∥平面BDC1;
(2)求证: 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径, ,
, 分别是
分别是 ,
, 的中点,
的中点, .
.
(1)证明: ;
;
(2)证明: ;
;
(3)假设这是个大容器,有条体积可以忽略不计的小鱼能在容器的任意地方游弋,如果鱼游到四棱锥 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF= AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.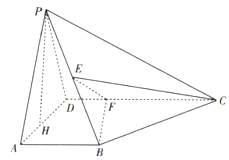
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=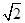 ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com