
分析 (Ⅰ)将圆心坐标代入椭圆方程,根据两点之间的距离公式,丨OT丨=$\sqrt{(1-\frac{{b}^{2}}{4}){x}_{0}^{2}+{b}^{2}-\frac{4}{3}}$≥$\sqrt{{b}^{2}-\frac{4}{3}}$,由切线长的最小值为$\frac{{\sqrt{6}}}{3}$,即可求得b的值,求得椭圆C的方程;
(Ⅱ)当斜率不存在,此时M、N分别为长、短轴一个端点,则△MON的面积为$\sqrt{2}$,当斜率存在,分别设出切线方程,代入求得M和N的坐标,由三角形的面积S△MON=${S}_{M{M}_{1}N{N}_{1}}$-${S}_{△OM{M}_{1}}$-${S}_{O{NN}_{1}}$,即可求得△MON的面积,方法二:设直线MN方程,代入椭圆方程,利用韦达定理及弦长公式,根据点到直线的距离公式及三角形的面积公式,即可求得△MON的面积为定值.
解答 解:(Ⅰ)如图1,因为椭圆$C:\frac{x^2}{4}+\frac{y^2}{b^2}=1(\frac{{2\sqrt{3}}}{3}<b<2)$,焦点在x轴上,P(x0,y0)在椭圆方程上,
则y02=b2(1-$\frac{{x}_{0}^{2}}{4}$),
由$\frac{2\sqrt{3}}{3}$<b<2,得:x02+y02=(1-$\frac{{b}^{2}}{4}$)x02+b2≥b2>$\frac{4}{3}$=r2,
故点O在圆P外,
不妨设OM与圆P相切于T,则有: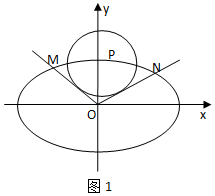
切线长丨OT丨=$\sqrt{丨OP{丨}^{2}-\frac{4}{3}}$=$\sqrt{{x}_{0}^{2}+{y}_{0}^{2}-\frac{4}{3}}$,__(1分)
代入得丨OT丨=$\sqrt{(1-\frac{{b}^{2}}{4}){x}_{0}^{2}+{b}^{2}-\frac{4}{3}}$≥$\sqrt{{b}^{2}-\frac{4}{3}}$,(3分)
由已知得:$\sqrt{{b}^{2}-\frac{4}{3}}$=$\sqrt{\frac{2}{3}}$,解得:b2=2,
所以椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$; (4分)
(Ⅱ)证明:1°当切线OM或ON斜率不存在即圆P与y轴相切时,易得丨x0丨=r=$\frac{2\sqrt{3}}{3}$,
代入椭圆方程得:丨x0丨=$\frac{2\sqrt{3}}{3}$,说明圆P同时也与x轴相切(图2),
此时M、N分别为长、短轴一个端点,则△MON的面积为$\sqrt{2}$.(5分)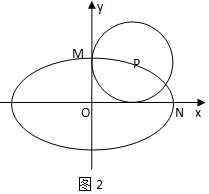
2°当切线OM、ON斜率都存在时,设切线方程为:y=kx,
由d=r得:$\frac{丨k{x}_{0}-{y}_{0}丨}{\sqrt{1+{k}^{2}}}$=$\frac{2}{\sqrt{3}}$,
整理得:(3x02-4)k2-6kx0y0+3y02-4=0(*),(6分)
由1°知:y02-4≠0,即丨x0丨≠$\frac{2\sqrt{3}}{3}$,此时丨y0丨≠$\frac{2\sqrt{3}}{3}$,方程(*)必有两个非零根,
记为k1,k2(k1<k2),则k1k2分别对应直线OM,ON的斜率,
由韦达定理得:k1k2=$\frac{3{y}_{0}^{2}-4}{3{x}_{0}^{2}-4}$,将x02=4-2y02,代入得:k1k2=$\frac{3{y}_{0}^{2}-4}{8-6{y}_{0}^{2}}$=-$\frac{1}{2}$ (7分)
解法一:(求交点坐标)
由上知:k1<0<k2,
设点N位于第一、三象限,点M位于第二、四象限,
若点N位于第一象限,点M位于第二象限,
设OM:y=k1x与椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$联立可得:M(-$\frac{2}{\sqrt{1+2{k}_{1}^{2}}}$,-$\frac{2{k}_{1}}{\sqrt{1+2{k}_{1}^{2}}}$)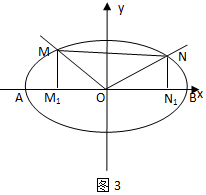
设ON:y=k2x与椭圆方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$联立可得:
N($\frac{2}{\sqrt{1+2{k}_{2}^{2}}}$,$\frac{2{k}_{2}}{\sqrt{1+2{k}_{2}^{2}}}$)(9分)
S△MON=${S}_{M{M}_{1}N{N}_{1}}$-${S}_{△OM{M}_{1}}$-${S}_{O{NN}_{1}}$=$\frac{1}{2}$(xN-xM)(yN+yM)-$\frac{1}{2}$(-xM)yM-$\frac{1}{2}$(xNyN)=$\frac{1}{2}$(xNyM-xMyN),(10分)
代入坐标有:
S△MON=2×$\frac{{k}_{2}-{k}_{1}}{\sqrt{1+2{k}_{1}^{2}}•\sqrt{1+2{k}_{2}^{2}}}$=2×$\sqrt{\frac{({k}_{2}-{k}_{1})^{2}}{(1+2{k}_{1}^{2})(1+2{k}_{2}^{2})}}$=2×$\sqrt{\frac{{k}_{1}^{2}+-2{k}_{1}{k}_{2}+{k}_{2}^{2}}{4{k}_{1}^{2}{k}_{2}^{2}+2{k}_{1}^{2}+2{k}_{2}^{2}+1}}$,
=2×$\sqrt{\frac{{k}_{1}^{2}+{k}_{2}^{2}+1}{2({k}_{1}^{2}+{k}_{2}^{2}+1)}}$=$\sqrt{2}$
同理,当点M、N位于其它象限时,结论也成立
综上,△MON的面积为定值$\sqrt{2}$.(12分)
解法二:(探寻直线MN方程特征)
(接上)设M(x1,y1)(x2,y2),
由于点P不与点A、B重合时,直线MN的斜率存在,不妨设直线MN的方程为:y=kx+m,
将MN与椭圆方程联立可得:(1+2k2)x2+4kmx+2m2-4=0,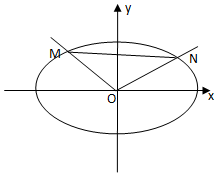
△=16k2m2-(1+2k2)(2m2-4)=32k2+16-8m2,
由△>0得4k2+2>m2,
由韦达定理可知:x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-4}{1+2{k}^{2}}$,(8分)
kOM•kON=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{2}$,
则x1x2+2y1y2=x1x2+2(kx1+m)(kx2+m)=(1+2k2)x1x2+2km(x1+x2)+2m2=0,
代入有:(1+2k2)$\frac{2{m}^{2}-4}{1+2{k}^{2}}$+2km(-$\frac{4km}{1+2{k}^{2}}$)+2m2=0,
整理得:m2=2k2+1; (9分)
又丨MN丨=$\sqrt{1+{k}^{2}}$丨x1-x2丨=$\sqrt{1+{k}^{2}}$$\frac{\sqrt{32{k}^{2}-8{m}^{2}+16}}{2{k}^{2}+1}$=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{16{k}^{2}+8}}{2{k}^{2}+1}$=2$\sqrt{2}$•$\frac{\sqrt{{k}^{2}+1}}{\sqrt{2{k}^{2}+1}}$,
而原点O到直线MN的距离为d=$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{1+2{k}^{2}}}{\sqrt{1+{k}^{2}}}$,(11分)
S△MON=$\frac{1}{2}$丨MN丨•d=$\frac{1}{2}$×2$\sqrt{2}$•$\frac{\sqrt{{k}^{2}+1}}{\sqrt{2{k}^{2}+1}}$×$\frac{\sqrt{1+2{k}^{2}}}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$.
所以△MON的面积为定值$\sqrt{2}$.(12分)
点评 本题考查椭圆的标准方程的求法,直线与圆、直线与圆锥曲线的位置关系,考查推理运算和方程求解能力.运用化归转化手段.将切线长最短问题转化为椭圆上的动点到定点距离最短问题;考查圆锥曲线中的有关定值问题,从变化中寻找不变量,并通过必要的推理和运算化简求值.考查转化化归思想、分类整合思想,属于难题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{7}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | $4+2\sqrt{2}$ | D. | $5+\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{10}{3}$ | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2,3} | ||
| C. | {3,4} | D. | {-3,-2,-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
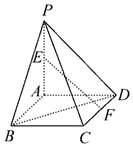 如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com