
分析 (a-2b-1)2+(a-c-lnc)2=0,可得a=2b+1,a=c+lnc.2b+1=c+lnc,|b-c|=$\frac{|1+c-lnc|}{2}$,令f(c)=1+c-lnc(c>0),利用导数研究函数的单调性极值与最值即可得出.
解答 解:∵(a-2b-1)2+(a-c-lnc)2=0,∴a=2b+1,a=c+lnc.
∴2b+1=c+lnc,
b=$\frac{c+lnc-1}{2}$.
∴|b-c|=$\frac{|1+c-lnc|}{2}$,
令f(c)=1+c-lnc(c>0),
f′(c)=1-$\frac{1}{c}$=$\frac{c-1}{c}$,
可得:c=1时,函数f(c)取得极小值即最小值,f(1)=2>0.
∴|b-c|=$\frac{|1+c-lnc|}{2}$≥1,
故答案为:1.
点评 本题考查了利用导数研究函数的单调性极值与最值、函数的性质、方程的解法,考查了推理能力与计算能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,6] | B. | (1,6] | C. | [-1,+∞) | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
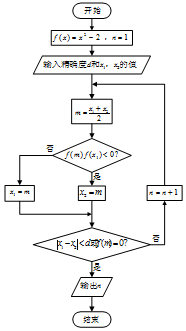 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com