
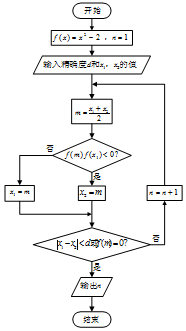
 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 按照用二分法求函数零点近似值得步骤求解即可.注意验证精确度的要求.
解答 解:模拟程序的运行,可得
n=1,x1=1,x2=2,d=0.1,
令f(x)=x2-2,则f(1)=-1<0,f(2)=2>0,
m=1.5,f(1.5)=0.25>0,满足条件f(m)f(x1)<0,x2=1.5,此时|1.5-1|=0.5>0.1,不合精确度要求.
n=2,m=1.25,f(1.25)=-0.4375<0.不满足条件f(m)f(x1)<0,x1=1.25,此时|1.5-1.25|=0.25>0.1,不合精确度要求.
n=3,m=1.375,f(1.375)=-0.109<0.不满足条件f(m)f(x1)<0,x1=1.375,此时|1.5-1.375|=0.125>0.1,不合精确度要求.
n=4,m=1.375,f(1.4375)=0.066>0.满足条件f(m)f(x1)<0,x2=1.4375,此时|1.5-1.4375|=0.062<0.1,符合精确度要求.
退出循环,输出n的值为4.
故选:C.
点评 本题主要考查用二分法求区间根的问题,属于基础题型.二分法是把函数的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而求零点近似值的方法.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
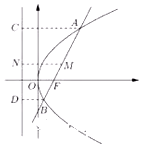 已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.
已知抛物线y2=4x的焦点为F,过焦点F的直线l交抛物线于A、B两点,设AB的中点为M,A、B、M在准线上的射影依次为C、D、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | ?-$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±$\frac{\sqrt{21}}{7}$x | D. | y=±$\frac{\sqrt{21}}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com