
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±$\frac{\sqrt{21}}{7}$x | D. | y=±$\frac{\sqrt{21}}{3}$x |
分析 设F1(-c,0),F2(c,0),则|F1P|=$\sqrt{{c}^{2}+4{b}^{2}}$,由F1、F2、P(0,2b)是正三角形的三个顶点可知|F1P|=$\sqrt{{c}^{2}+4{b}^{2}}$=2c,由此可求出b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,进而得到双曲线的渐近线方程.
解答 解:若F1,F2,P(0,2b)是正三角形的三个顶点,
设F1(-c,0),F2(c,0),则|F1P|=$\sqrt{{c}^{2}+4{b}^{2}}$,
∵F1、F2、P(0,2b)是正三角形的三个顶点,
∴$\sqrt{{c}^{2}+4{b}^{2}}$=2c,∴c2+4b2=4c2,
∴c2+4(c2-a2)=4c2,
∴c2=4a2,即c=2a,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,
∴双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\sqrt{3}$x.
故选:B.
点评 本题考查双曲线的性质,主要是渐近线方程的求法,在解题时要注意审题,由F1、F2、P(0,2b)是正三角形的三个顶点建立方程,考查运算能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
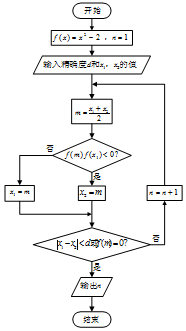 二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )
二分法是求方程近似解的一种方法,其原理是“一分为二,无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.1,则输出n的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至30岁 | 6 | 14 | 20 | 32 | 40 | 48 |
| 31岁至44岁 | 4 | 6 | 20 | 28 | 40 | 42 |
| 45岁至59岁 | 22 | 18 | 33 | 37 | 19 | 11 |
| 60岁及以上 | 15 | 13 | 10 | 12 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com