Question

17．四面体的一条棱长为x，余下的棱长均为1．
（1）把四面体的体积V表示为x的函数f（x）并求出定义域；
（2）求体积V的最大值．

Answer 1

分析 （1）取AD中点E，BC中点F，证明BC⊥面AFD，及EF⊥AD，利用V=$\frac{1}{3}$BC?S_△AFD，可把四面体的体积V表示为x的函数f（x）并求出定义域；
（2）利用配方法求体积V的最大值．

解答 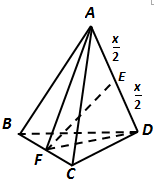解：如图四面体ABCD中，AD=x，其余各棱为1．取AD中点E，BC中点F
证明BC⊥面AFD，及EF⊥AD
在三角形ABC中，∵三角形ABC为正三角形，F点是BC的中点，
∴AF⊥BC
同理FD⊥BC
∵AF∩FD=F，∴BC⊥面AFD…．（3分）
（1）V=$\frac{1}{3}$BC?S_△AFD=$\frac{1}{3}$?BC?$\frac{1}{2}$AD?EF=$\frac{1}{6}$BC?AD?EF=$\frac{1}{6}$?1?x?$\sqrt{（\frac{\sqrt{3}}{2}）^{2}-（\frac{x}{2}）^{2}}$
=$\frac{1}{12}$x$\sqrt{3-{x}^{2}}$
即f（x）=$\frac{1}{12}$x$\sqrt{3-{x}^{2}}$，…．（7分）
其中定义域为 x∈（0，$\sqrt{3}$）…．（8分）
（2）V=$\frac{1}{12}$$\sqrt{3{x}^{2}-{x}^{4}}$=$\frac{1}{12}$$\sqrt{-（{x}^{2}-\frac{3}{2}）^{2}+\frac{9}{4}}$，当x=$\frac{\sqrt{6}}{2}$时，V_max=$\frac{1}{8}$…．（12分）

点评 本题考查体积的计算，考查配方法，考查学生分析解决问题的能力，正确求体积是关键．