
【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示. 
(1)求图中x的值,并根据频率分布直方图估计这500名志愿者中年龄在[35,40)岁的人数;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为X,求X的分布列及数学期望.
【答案】
(1)解:根据频率分布直方图的性质可得:(0.01+0.02+0.04+x+0.07)×5=1,解得x=0.06.
估计这500名志愿者中年龄在[35,40)岁的人数=0.06×5×500=150人
(2)解:用分层抽样的方法,从100名志愿者中选取10名,
则其中年龄“低于35岁”的人有6名,
“年龄不低于35岁”的人有4名.
故X的可能取值为0,1,2,3,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=3)= ![]() =
= ![]() .
.
故X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EX=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =1.8
=1.8
【解析】(1)根据小矩形的面积等于频率,而频率之和等于0.即可得出x,再用频率×总体容量即可.(2)分层抽样的方法,从100名志愿者中选取10名;则其中年龄“低于35岁”的人有10×(0.01+0.04+0.07)×5=6名,“年龄不低于35岁”的人有4名.X的可能取值为0,1,2,3,再利用超几何分布即可得出,再利用数学期望的计算公式即可得出.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某海警基地码头O的正东方向40海里处有海礁界碑M,过点M且与OM成![]() (即北偏西
(即北偏西![]() )的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东
)的直线l在在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东![]() 方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留. 基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.
(1)如果O和A相距6海里,求可疑船被截获处的点P的轨迹;
(2)若要确保在领海内捕获可疑船(即P不能在公海上).则![]() 、
、![]() 之间的最大距离是多少海里?
之间的最大距离是多少海里?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的双曲线![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点
恒有两个不同的交点![]() 和
和![]() ,且
,且![]() (其中
(其中![]() 为坐标原点),求实数
为坐标原点),求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
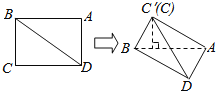
【题目】如图所示,在矩形ABCD中,![]() ,
,![]() 沿对角线将
沿对角线将![]() 折起,使点C移到
折起,使点C移到![]() 点,且C点在平面ABD的射影O恰在AB上.
点,且C点在平面ABD的射影O恰在AB上.
(1)求证:![]() 平面ACD;
平面ACD;
![]() 求直线AB与平面
求直线AB与平面![]() D所成角的正弦值.
D所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的![]() 进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按
进行奖励;当销售利润超过15万元时,若超过部分为A万元,则超出部分按![]() 进行奖励,没超出部分仍按销售利润的
进行奖励,没超出部分仍按销售利润的![]() 进行奖励
进行奖励![]() 记奖金总额为
记奖金总额为![]() 单位:万元
单位:万元![]() ,销售利润为
,销售利润为![]() 单位:万元
单位:万元![]() .
.
![]() 1
1![]() 写出该公司激励销售人员的奖励方案的函数表达式;
写出该公司激励销售人员的奖励方案的函数表达式;
![]() 2
2![]() 如果业务员老张获得
如果业务员老张获得![]() 万元的奖金,那么他的销售利润是多少万元?
万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
已知圆满足:
① 截y轴所得弦长为2;
②被x轴分成两段圆弧,其弧长的比为3:1;
③圆心到直线l:x-2y=0的距离为![]() ,求该圆的方程.
,求该圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线C:y2=nx(n>0)在第一象限内的点P(2,t)到焦点的距离为 ![]() ,曲线C在点P处的切线交x轴于点Q,直线l1经过点Q且垂直于x轴.
,曲线C在点P处的切线交x轴于点Q,直线l1经过点Q且垂直于x轴.
(Ⅰ)求线段OQ的长;
(Ⅱ)设不经过点P和Q的动直线l2:x=my+b交曲线C于点A和B,交l1于点E,若直线PA,PE,PB的斜率依次成等差数列,试问:l2是否过定点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com