
| 1 |
| 1-x |
| 1 |
| 1-x |
|
| 1 |
| 1-x |
| 1 |
| 1-x |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |


科目:高中数学 来源: 题型:
|
| A、(1,+∞) |
| B、(0,1) |
| C、(-1,1) |
| D、(-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
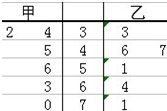 近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表:
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康.其形成与PM2.5有关.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值越小,空气质量越好.为加强生态文明建设,我国国家环保部于2012年2月29日,发布了《环境空气质量标准》见表:| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k≤75 | 二级 |
| k>75 | 超标 |
查看答案和解析>>
科目:高中数学 来源: 题型:
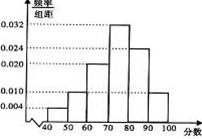 某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.
某校高三年级发展均衡,各班均有学生50人,全校共有20个平行班级.随机选择一个班,将他们的期中数学考试成绩分成六段:[40,50),[50,60),…,[90,100],得到如图所示频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com