
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)设![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,函数
,函数![]() ,试判断是否存在
,试判断是否存在![]() ,使得
,使得![]() 为函数
为函数![]() 的极小值点.
的极小值点.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
【题目】近年来,太阳能技术运用的步伐日益加快.2002年全球太阳能电池的年生产量达到670 MW,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳能电池的年生产量(结果精确到0.1 MW);
(2)目前太阳能电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420MW.假设以后若干年内太阳能电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳能电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技公司研究开发了一种新产品,生产这种新产品的每天固定成本为![]() 元,每生产
元,每生产![]() 件,需另投入成本为
件,需另投入成本为![]() 元,
元, 每件产品售价为
每件产品售价为![]() 元(该新产品在市场上供不应求可全部卖完).
元(该新产品在市场上供不应求可全部卖完).
(1)写出每天利润![]() 关于每天产量
关于每天产量![]() 的函数解析式;
的函数解析式;
(2)当每天产量为多少件时,该公司在这一新产品的生产中每天所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”,分初赛和复赛两个阶段进行,规定:初赛成绩大于90分的具有复赛资格,某校有800名学生参加了初赛,所有学生的成绩均在区间(30,150]内,其频率分布直方图如图.则获得复赛资格的人数为()

A.640B.520C.280D.240
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(![]() )当
)当![]() 时,求此函数对应的曲线在
时,求此函数对应的曲线在![]() 处的切线方程.
处的切线方程.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )对
)对![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() ;(
;(![]() )见解析;(
)见解析;(![]() )当
)当![]() 时,
时, ![]() ,当
,当![]() 时
时![]()
【解析】试题分析:(1)利用导数的意义,求得切线方程为![]() ;(2)求导得
;(2)求导得![]() ,通过
,通过![]() ,
, ![]() ,
, ![]() 分类讨论,得到单调区间;(3)分离参数法,得到
分类讨论,得到单调区间;(3)分离参数法,得到![]() ,通过求导,得
,通过求导,得![]() ,
, ![]() .
.
试题解析:
(![]() )当
)当![]() 时,
时, ![]() ,
,
∴![]() ,
, ![]() ,
,
![]() ,∴切线方程
,∴切线方程![]() .
.
(![]() )
)![]()
![]()
![]() .
.
令![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上为增函数.
上为增函数.
在![]() 上为减函数,
上为减函数,
当![]() 时,
时, ![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时, ![]() 在
在![]() ,
, ![]() 上为单调递增,
上为单调递增,
在![]() 上单调递减.
上单调递减.
(![]() )当
)当![]() 时,
时, ![]() ,
,
当![]() 时,由
时,由![]() 得
得
![]() ,对
,对![]() 恒成立.
恒成立.
设![]() ,则
,则
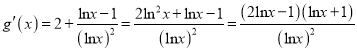 ,
,
令![]() 得
得![]() 或
或![]() ,
,
|
|
|
|
|
|
|
|
|
| 极小 |
|
![]() ,∴
,∴![]() ,
, ![]() .
.
点睛:本题考查导数在函数综合题型中的应用。含参的函数单调性讨论,考查学生的分类讨论能力,本题中,结合导函数的形式,分类讨论;含参的恒成立问题,一般采取分离参数法,解决恒成立。
【题型】解答题
【结束】
20
【题目】已知集合![]() ,集合
,集合![]() 且满足:
且满足:
![]() ,
, ![]() ,
, ![]() 与
与![]() 恰有一个成立.对于
恰有一个成立.对于![]() 定义
定义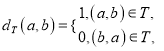
![]() .
.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的值及
的值及![]() 的最大值.
的最大值.
(![]() )取
)取![]() ,
, ![]() ,
, ![]() ,
, ![]() 中任意删去两个数,即剩下的
中任意删去两个数,即剩下的![]() 个数的和为
个数的和为![]() ,求证:
,求证: ![]() .
.
(![]() )对于满足
)对于满足![]() 的每一个集合
的每一个集合![]() ,集合
,集合![]() 中是否都存在三个不同的元素
中是否都存在三个不同的元素![]() ,
, ![]() ,
, ![]() ,使得
,使得![]() 恒成立,并说明理由.
恒成立,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com