考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)AD∥BC,可得∠DAE就是异面直线AE与BC所成角,解三角形即可求得结果;
(2)取BB1的中点F,连接AF、CF、EF.可以证出四边形B1FCE是平行四边形,从而CF∥B1E;然后再证四边形ADEF是平行四边形,可得AF∥ED,结合面面平行的判定定理,得到平面ACF∥平面B1DE. 最后利用面面平行的性质,得到AC∥面B1DE;
(3)转换底面,底为面ABD,高为EC,由体积公式求得三棱锥A-BDE的体积.
解答:
(1)解:由题意,AD∥BC,
∴∠DAE就是异面直线AE与BC所成角,
在△RtADE中,由于DE=
,AD=2,可得AE=3
∴cos∠DAE=
=
;
(2)证明:取BB
1的中点F,连接AF、CF、EF.
∵E、F是C
1C、B
1B的中点,
∴CE∥B
1F且CE=B
1F
∴四边形B
1FCE是平行四边形,
∴CF∥B
1E.
∵正方形BB
1C
1C中,E、F是CC、BB的中点,
∴EF∥BC且EF=BC
又∵BC∥AD且BC=AD,
∴EF∥AD且EF=AD.
∴四边形ADEF是平行四边形,可得AF∥ED,
∵AF∩CF=C,BE∩ED=E,
∴平面ACF∥平面B
1DE. 又∵AC?平面ACF,
∴AC∥面B
1DE.
(3)解:∵AC∥面B
1DE
∴A到面B
1DE 的距离等于C到面B
1DE 的距离,
∴V
A-B1DE=V
C-B1DE=V
D-B1DC=
••1•2•2=
.
点评:本题以正方体为平台,着重考查了空间直线与平面平行的判定与性质,考查异面直线所成角问题,求解方法一般是平移法,转化为平面角问题来解决,体现了数形结合和转化的思想.

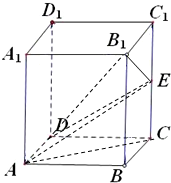 在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点
在棱长为2的正方体ABCD-A1B1C1D1中,点E是棱CC1中点

 阅读快车系列答案
阅读快车系列答案 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,已知每个元件正常工作的概率均为
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,已知每个元件正常工作的概率均为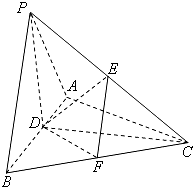 如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.
如图,在三棱锥P-ABC中,△PAB是等边三角形,D、E分别为AB、PC的中点.