
| A. | [-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,0) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(0,+∞) |
分析 由题意可得,线段PQ的中点为M(x0,y0)到两直线的距离相等,利用$\frac{|{x}_{0}+3{y}_{0}-2|}{\sqrt{10}}=\frac{|{x}_{0}+3{y}_{0}+6|}{\sqrt{10}}$,可得x0+3y0+2=0.
又y0<x0+2,设$\frac{y_0}{x_0}$=kOM,分类讨论:当点位于线段AB(不包括端点)时,当点位于射线BM(不包括端点B)时,即可得出.
解答  解:∵点P在直线x+3y-2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),
解:∵点P在直线x+3y-2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),
∴$\frac{|{x}_{0}+3{y}_{0}-2|}{\sqrt{10}}=\frac{|{x}_{0}+3{y}_{0}+6|}{\sqrt{10}}$,化为x0+3y0+2=0.
又y0<x0+2,
设$\frac{{y}_{0}}{{x}_{0}}$=kOM,
当点位于线段AB(不包括端点)时,则kOM>0,当点位于射线BM(不包括端点B)时,kOM<-$\frac{1}{3}$.
∴$\frac{{y}_{0}}{{x}_{0}}$的取值范围是(-∞,-$\frac{1}{3}$)∪(0,+∞).
故选:D.
点评 本题考查了平行线的性质、点到直线的距离公式、线性规划的知识、斜率的意义及其应用,考查了数形结合的思想方法、计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
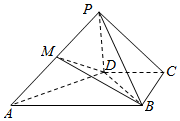 在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=4,AB∥CD,∠BCD=90°,M为棱PA的中点.
在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=4,AB∥CD,∠BCD=90°,M为棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 24 | C. | 6 | D. | -24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com