
分析 作函数f(x)=$\left\{\begin{array}{l}|{ln(-x)}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象,从而可化为x2-2bx+3=0在(0,3]上有两个不同的解;而m(x)=$\frac{x}{2}$+$\frac{3}{2x}$在(0,$\sqrt{3}$)上是减函数,在($\sqrt{3}$,3]上是增函数;从而解得.
解答 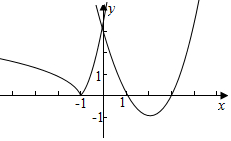 解:作函数f(x)=$\left\{\begin{array}{l}|{ln(-x)}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象如下,
解:作函数f(x)=$\left\{\begin{array}{l}|{ln(-x)}|,x<0\\{x^2}-4x+3,x≥0\end{array}\right.$的图象如下,
,∵H(x)=[f(x)]2-2bf(x)+3有8个不同的零点,
∴g(x)=x2-2bx+3在(0,3]上有两个零点;
即x2-2bx+3=0在(0,3]上有两个不同的解;
故b=$\frac{{x}^{2}+3}{2x}$=$\frac{x}{2}$+$\frac{3}{2x}$在(0,3]上有两个不同的解;
而m(x)=$\frac{x}{2}$+$\frac{3}{2x}$在(0,$\sqrt{3}$)上是减函数,在($\sqrt{3}$,3]上是增函数;
而m($\sqrt{3}$)=$\sqrt{3}$,m(3)=2;
故$\sqrt{3}$<b≤2,
故答案为:($\sqrt{3}$,2].
点评 本题考查了分类讨论的思想应用及数形结合的思想应用,同时考查了函数的零点与方程的根的关系应用.


科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,2) | C. | (0,2) | D. | [2.3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
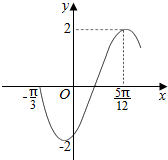
| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | 4,-$\frac{π}{6}$ | D. | 4,$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{3}$,0) | B. | (-$\frac{1}{3}$,0) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-$\frac{1}{3}$)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)≥2-4ln2 | B. | f(x)≤2-4ln2 | C. | f(x)≥4-8ln2 | D. | f(x)≤4-8ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
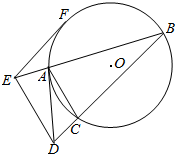 如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.
如图所示,△ABC内接于⊙O,直线AD与⊙O相切于点A,交BC的延长线于点D,过点D作DE∥CA交BA的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com