
【题目】已知动点M(x,y)满足![]() ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(1)求E的标准方程;
(2)过点F(1,0)作直线交曲线E于P,Q两点,交![]() 轴于R点,若
轴于R点,若![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)-4.
;(2)-4.
【解析】分析:(Ⅰ)由![]() ,根据椭圆的定义可得点
,根据椭圆的定义可得点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,可求得
为焦点的椭圆,可求得![]() ,从而可得曲线
,从而可得曲线![]() 的方程;(II)设
的方程;(II)设![]() ,由
,由![]() ,点
,点![]() 在曲线
在曲线![]() 上可得
上可得![]() …,①同理可得
…,①同理可得![]() …,②,由①②可得
…,②,由①②可得![]() 是方程
是方程![]() 的两个根,
的两个根,![]() 为定值
为定值![]() .
.
详解:(Ⅰ)由![]() ,
,
可得点M(x,y)到定点A(﹣1,0),B(1,0)的距离等于之和等于![]() .
.
且AB![]() ,所以动点N的轨迹是以C(﹣1,0),A(1,0)为焦点的椭圆,
,所以动点N的轨迹是以C(﹣1,0),A(1,0)为焦点的椭圆,
且长轴长为![]() ,焦距2c=2,所以,c=1,b=1,曲线E的方程为:
,焦距2c=2,所以,c=1,b=1,曲线E的方程为:![]() ;
;
(Ⅱ)法1:设P(x1,y1),Q(x2,y2),R(0,y0),
由![]() ,(x1,y1﹣y0)=λ1(1﹣x1,﹣y1),∴
,(x1,y1﹣y0)=λ1(1﹣x1,﹣y1),∴![]() ,
,
∵过点F(1,0)作直线l交曲线E于P,∴![]() ,
,
∴![]() …①
…①
同理可得:![]() …②
…②
由①②可得λ1、λ2是方程x2+4x+2﹣2y02=0的两个根,∴λ1+λ2为定值﹣4.
法2:依题意得![]() 的斜率一定存在,设斜率为k,
的斜率一定存在,设斜率为k,
则直线方程为![]() 代入椭圆方程得:
代入椭圆方程得:![]()
设![]() ,则
,则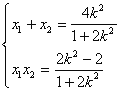 ,
,
由![]() 得:
得:![]() 得
得![]()
同理得:![]()
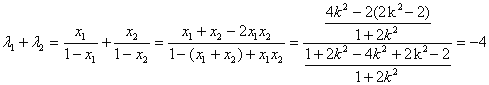
则![]() 为定值。
为定值。


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】已知点F(1,0),点A是直线l1:x=﹣1上的动点,过A作直线l2 , l1⊥l2 , 线段AF的垂直平分线与l2交于点P. (Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若点M,N是直线l1上两个不同的点,且△PMN的内切圆方程为x2+y2=1,直线PF的斜率为k,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M(x1 , f(x1))和点N(x2 , g(x2))分别是函数f(x)=ex﹣ ![]() x2和g(x)=x﹣1图象上的点,且x1≥0,x2>0,若直线MN∥x轴,则M,N两点间的距离的最小值为( )
x2和g(x)=x﹣1图象上的点,且x1≥0,x2>0,若直线MN∥x轴,则M,N两点间的距离的最小值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的分别为a,b,c,且acosB=(3c﹣b)cosA.
(1)若asinB=2 ![]() ,求b;
,求b;
(2)若a=2 ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京某附属中学为了改善学生的住宿条件,决定在学校附近修建学生宿舍,学校总务办公室用1000万元从政府购得一块廉价土地,该土地可以建造每层1000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高0.02万元,已知建筑第5层楼房时,每平方米建筑费用为0.8万元.
(1)若学生宿舍建筑为![]() 层楼时,该楼房综合费用为
层楼时,该楼房综合费用为![]() 万元,综合费用是建筑费用与购地费用之和),写出
万元,综合费用是建筑费用与购地费用之和),写出![]() 的表达式;
的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,学校应把楼层建成几层?此时平均综合费用为每平方米多少万元?
【答案】(1)![]() ;(2)学校应把楼层建成
;(2)学校应把楼层建成![]() 层,此时平均综合费用为每平方米
层,此时平均综合费用为每平方米![]() 万元
万元
【解析】
![]() 由已知求出第
由已知求出第![]() 层楼房每平方米建筑费用为
层楼房每平方米建筑费用为![]() 万元,得到第
万元,得到第![]() 层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高
层楼房建筑费用,由楼房每升高一层,整层楼建筑费用提高![]() 万元
万元![]() ,然后利用等差数列前
,然后利用等差数列前![]() 项和求建筑
项和求建筑![]() 层楼时的综合费用
层楼时的综合费用![]() ;
;
![]() 设楼房每平方米的平均综合费用为
设楼房每平方米的平均综合费用为![]() ,则
,则![]() ,然后利用基本不等式求最值.
,然后利用基本不等式求最值.
解:![]() 由建筑第5层楼房时,每平方米建筑费用为
由建筑第5层楼房时,每平方米建筑费用为![]() 万元,
万元,
且楼房每升高一层,整层楼每平方米建筑费用提高![]() 万元,
万元,
可得建筑第1层楼房每平方米建筑费用为:![]() 万元.
万元.
建筑第1层楼房建筑费用为:![]() 万元
万元![]() .
.
楼房每升高一层,整层楼建筑费用提高:![]() 万元
万元![]() .
.
建筑第x层楼时,该楼房综合费用为:![]() .
.
![]() ;
;
![]() 设该楼房每平方米的平均综合费用为
设该楼房每平方米的平均综合费用为![]() ,
,
则:![]() ,
,
当且仅当![]() ,即
,即![]() 时,上式等号成立.
时,上式等号成立.
![]() 学校应把楼层建成10层,此时平均综合费用为每平方米
学校应把楼层建成10层,此时平均综合费用为每平方米![]() 万元.
万元.
【点睛】
本题考查简单的数学建模思想方法,训练了等差数列前n项和的求法,训练了利用基本不等式求最值,是中档题.
【题型】解答题
【结束】
20
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)对称轴为![]() ,最小正周期
,最小正周期![]() ;(2)
;(2)![]()
【解析】
(1)利用正余弦的二倍角公式和辅助角公式将函数解析式进行化简得到![]() ,由周期公式和对称轴公式可得答案;(2)由x的范围得到
,由周期公式和对称轴公式可得答案;(2)由x的范围得到![]() ,由正弦函数的性质即可得到值域.
,由正弦函数的性质即可得到值域.
(1)![]()
![]()
令![]() ,则
,则
![]() 的对称轴为
的对称轴为![]() ,最小正周期
,最小正周期![]() ;
;
(2)当![]() 时,
时,![]() ,
,
因为![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
在![]() 取最大值,在
取最大值,在![]() 取最小值,
取最小值,
所以![]() ,
,
所以![]() .
.
【点睛】
本题考查正弦函数图像的性质,考查周期性,对称性,函数值域的求法,考查二倍角公式以及辅助角公式的应用,属于基础题.
【题型】解答题
【结束】
21
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2+ax+a). (I)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增大,下表是该地一农业银行连续五年的储蓄存款(年底余额),如下表:

为了研究方便,工作人员将上表的数据进行了处理,![]() ,得到下表:
,得到下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?
(附:线性回归方程:![]() ,
,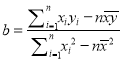 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com