
分析 先求出矩阵M-1,再设曲线C上任意一点P(x,y)在矩阵M-1对应的变换下得到P'(x',y'),根据矩阵的性质即可求出答案.
解答 解::${M^{-1}}=[{\begin{array}{l}{\frac{1}{2}}&0\\ 0&{\frac{1}{3}}\end{array}}]$,设曲线C上任意一点P(x,y)在矩阵M-1对应的变换下得到P'(x',y'),
则$[{\begin{array}{l}{\frac{1}{2}}&0\\ 0&{\frac{1}{3}}\end{array}}][{\begin{array}{l}x\\ y\end{array}}]=[{\begin{array}{l}{x'}\\{y'}\end{array}}]$,即$\left\{{\begin{array}{l}{\frac{1}{2}x=x'}\\{\frac{1}{3}y=y'}\end{array}}\right.$,因此$\left\{{\begin{array}{l}{x=2x'}\\{y=3y'}\end{array}}\right.$,
因为点P(x,y)满足曲线C:x2+y2=1,
所以有4x'2+9y'2=1,
因此可得在矩阵M-1所对应的线性变换作用下的曲线方程为4x2+9y2=1
点评 本题考查矩阵变换的应用,考查逆矩阵的求法.解题时要认真审题,仔细解答.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,1] | C. | [0,3] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-2,2) | C. | (-1,5) | D. | (-2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
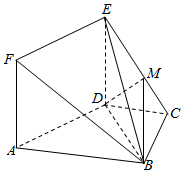 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,CD=BC=$\frac{1}{2}$AB=1,点M在线段EC上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
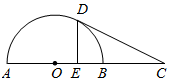 如图,AB是半圆O的直径,延长AB到C,使BC=$\sqrt{2}$,CD切半圆O于点D,DE⊥AB,垂足为E.若AE:EB=3:1,求DE的长.
如图,AB是半圆O的直径,延长AB到C,使BC=$\sqrt{2}$,CD切半圆O于点D,DE⊥AB,垂足为E.若AE:EB=3:1,求DE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com