
四棱锥A-BCDE的正视图和俯视图如下,其中俯视图是直角梯形.
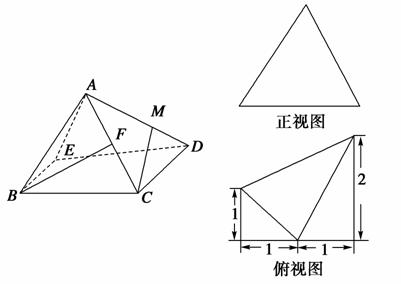
(1)若正视图是等边三角形,F为AC的中点,当点M在棱AD上移动时,是否总有BF丄CM,请说明理由;
(2)若AB=AC,平面ABC与平面ADE所成的锐二面角为45°,求直线AD与平面ABE所成角的正弦值.
[解析] (1)总有BF⊥CM,理由如下:
法一:取BC的中点O,连接AO,
由俯视图可知,AO⊥平面BCDE,CD⊂平面BCDE,
所以AO⊥CD.
又CD⊥BC,所以CD⊥平面ABC,故CD⊥BF.
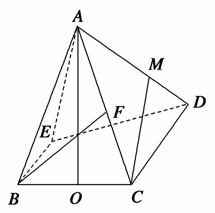
因为△ABC为正三角形,F是AC的中点,
所以BF⊥AC.
又AC∩CD=D,故BF⊥平面ACD,
因为CM⊂平面ACD,所以BF⊥CM.
法二:取BC的中点O,连接AO,由俯视图可知,AO⊥平面BCDE,取DE中点H,连接OH,OH⊥BC,
以OC、OH、OA分别为x轴、y轴、z轴建立空间直角坐标系O-xyz.
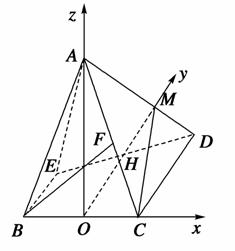
则A(0,0,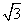 ),B(-1,0,0),C(1,0,0),D(1,2,0),可求得F(
),B(-1,0,0),C(1,0,0),D(1,2,0),可求得F(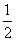 ,0,
,0,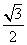 ),
),
设点M的横坐标为x,可求得点M(x,2x,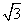 (1-x))
(1-x))
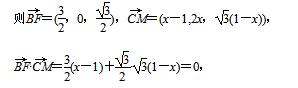 故BF⊥CM.
故BF⊥CM.
(2)建系同上,设A(0,0,a),(a>0),
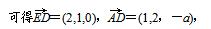 设平面ADE的法向量为m=(x1,y1,z1),
设平面ADE的法向量为m=(x1,y1,z1),
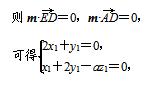 取x1=1,y1=-2,z1=-
取x1=1,y1=-2,z1=-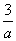 ,
,
可得m=(1,-2,-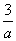 ).
).
又平面ABC的法向量为n=(0,1,0),
 设平面ABE的法向量为p=(x2,y2,z2),
设平面ABE的法向量为p=(x2,y2,z2),
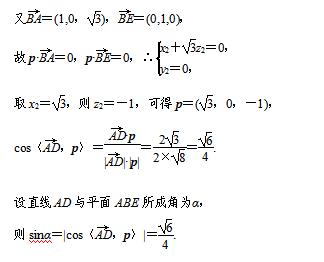


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
若直线l不平行于平面α,且l⊄α,则( )
A.α内的所有直线与l异面
B.α内不存在与l平行的直线
C.α内存在唯一的直线与l平行
D.α内的直线与l都相交
查看答案和解析>>
科目:高中数学 来源: 题型:
(2013·盐城模拟)如图,P为▱ABCD所在平面外一点,M,N分别为AB,PC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
 [
[
查看答案和解析>>
科目:高中数学 来源: 题型:
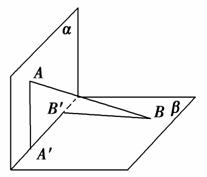
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为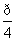 和
和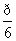 ,过A,B两点分别作两平面交线的垂线,垂足为A′、B′,若AB=12,则A′B′的长为( )
,过A,B两点分别作两平面交线的垂线,垂足为A′、B′,若AB=12,则A′B′的长为( )
A.4 B.6
C.8 D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在几何体ABCDE中,AB=AD=2,AB⊥AD,AE⊥平面ABD.M为线段BD的中点,MC∥AE,AE=MC=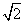 .
.
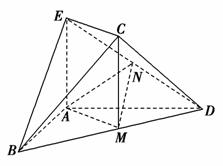
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC的三边长分别为AB=5,BC=4,AC=3,M是AB边上的高,P是平面ABC外一点.给出下列四个命题:
①若PA⊥平面ABC,则三棱锥P-ABC的四个面都是直角三角形;
②若PM⊥平面ABC,且M是AB边的中点,则有PA=PB=PC;
③若PC=5,PC⊥平面ABC,则△PCM面积的最小值为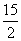 ;
;
④若PC=5,P在平面ABC上的射影是△ABC的内切圆的圆心,则点P到平面ABC的距离为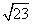 .
.
其中正确命题的序号是________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
若空间中有四个点,则“这四个点中有三点在同一条直线上”是“这四个点在同一个平面上”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
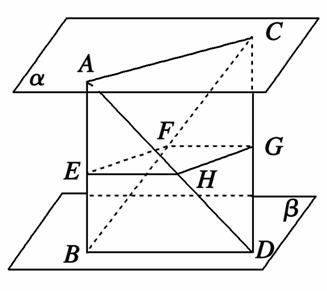
如图,已知α∥β,异面直线AB,CD和平面α,β分别交于A,B,C,D四点,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:(1)E,F,G,H共面;
(2)平面EFGH∥平面α.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com