直线(1+3m)x+(3-2m)y+8m-12＝0(m∈R)与圆x2+y2-2x-6y+1＝0的交点个数为( ) A．1 B．2 C．0或2 D．1或2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

直线(1＋3m)x＋(3－2m)y＋8m－12＝0(m∈R)与圆x²＋y²－2x－6y＋1＝0的交点个数为(　　)

A．1 B．2 C．0或2 D．1或2

解析　将含参直线方程分离变量可得m(3x－2y＋8)＋x＋3y－12＝0，

不论m取何值，直线恒过两直线的交点A(0,4)，

又易知定点A在圆内，故直线必与圆恒相交，故选B.

练习册系列答案

Happy holiday快乐假期寒电子科技大学出版社系列答案

暑假作业自主开放有趣实效江西高校出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

已知f(x)是定义在R上且周期为3的函数，当x∈[0,3)时，f(x)＝|x²－2x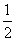＋|.若函数y＝f(x)－a在区间[－3,4]上有10个零点(互不相同)，则实数a的取值范围是________．

查看答案和解析>>

科目：高中数学 来源： 题型：

已知函数.

(1)若函数在上为增函数，求实数a的取值范围；

(2)当时，求在上的最大值和最小值；

(3)求证：对任意大于1的正整数n，恒成立.

查看答案和解析>>

科目：高中数学 来源： 题型：

已知平面α，β，直线l，若α⊥β，α∩β＝l，则(　　)

A．垂直于平面β的平面一定平行于平面α

B．垂直于直线l的直线一定垂直于平面α

C．垂直于平面β的平面一定平行于直线l

D．垂直于直线l的平面一定与平面α，β都垂直

查看答案和解析>>

科目：高中数学 来源： 题型：

为保增长、促发展，某地计划投资甲、乙两项目，市场调研得知，甲项目每投资百万元需要配套电能2万千瓦，可提供就业岗位24个，增加GDP 260万元；乙项目每项投资百万元需要配套电能4万千瓦，可提供就业岗位32个，增加GDP 200万元，已知该地为甲、乙两项目最多可投资3 000万元，配套电能100万千瓦，并要求它们提供的就业岗位不少于800个，如何安排甲、乙两项目的投资额，增加的GDP最大？

查看答案和解析>>

科目：高中数学 来源： 题型：

命题“∃x∈R,2x²－3ax＋9<0”为假命题，则实数a的取值范围是________．

查看答案和解析>>

科目：高中数学 来源： 题型：

定义：|a×b|＝|a||b|sin θ，其中θ为向量a与b的夹角，若|a|＝2，|b|＝5，a·b＝－6，则|a×b|等于(　　)