
����Ŀ�������Ŵ���ij����̨�Ƴ�����Ϸ��Ŀ��ѡ�����1��8��8�ȴ��ţ����ΰ������ϵ����壬����Ქ��һ�����֣���һ�������и����Ե���ɫ���ɵķ�ʽ�����ѡ������ȷ�ش����������֣����ɻ�ø����Ŷ�Ӧ�ļ�ͥ���������һ�γ�������У����ֲ���ѡ�ֶ�����Ϊ��������Σ�20��30��30��40����λ���꣩����¶Ը�����������������ͼ��ʾ�� 
��1��д��2��2���������ж��Ƿ���90%�İ�����Ϊ�¶Ը����������������йأ�˵��������ɣ���������ٽ�ֵ�����ο��� ���ο���ʽ��K2= ![]() ������n=a+b+c+d��
������n=a+b+c+d��
P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
��2���ּƻ�����γ�������а������ѡȡ6��ѡ�֣�����ȡ3������ѡ�֣���3������ѡ������20��30��֮��������ķֲ��к���ѧ������
���𰸡�
��1���⣺
����/���� | ��ȷ | ���� | �ϼ� |
20��30 | 10 | 30 | 40 |
30��40 | 10 | 70 | 80 |
�ϼ� | 20 | 100 | 120 |
K2= ![]() =3��2.706
=3��2.706
����90%�İ�����Ϊ�¶Ը����������������й�
��2���⣺��3��ѡ������20��30��֮�������Ϊ�Σ�����ȡֵΪ0��1��2������5�֣�
20��30��֮���������2��
P����=0��= ![]() =
= ![]() ��P����=1��=
��P����=1��= ![]() =
= ![]() ��P����=2��=
��P����=2��= ![]() =
= ![]()
�� | 0 | 1 | 2 |
P |
|
|
|
E��=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() =1
=1
����������1�����������Ķ�ά����ͼ�õ������������ù�ʽ���k2=3��2.706�����ɵó����ۣ���2��ȷ��������ȡֵ�������Ӧ�ĸ��ʣ�������3������ѡ������20��30��֮��������ķֲ��к���ѧ������
�����㾫�������ڱ��⿼���Ƶ�ʷֲ�ֱ��ͼ����Ҫ�˽�Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ���ܵó���ȷ�𰸣�


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ����
����![]() .
.
��1�����![]() �Ĺ켣
�Ĺ켣![]() �ķ���
�ķ���
��2������![]() ��ֱ�߽��켣
��ֱ�߽��켣![]() ��
��![]() ���㣬
���㣬![]() Ϊ
Ϊ![]() ������һ�㣬ֱ��
������һ�㣬ֱ��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() Ϊֱ����Բ�Ƿ��
Ϊֱ����Բ�Ƿ��![]() ���ϵĶ��㣿 �������㣬�����������ꣻ���������㣬˵�����ɡ�
���ϵĶ��㣿 �������㣬�����������ꣻ���������㣬˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABC�У�PA��AB��PA��BC��AB��BC��PA��AB��BC��2��DΪ�߶�AC���е㣬EΪ�߶�PC��һ��.

(1)��֤��PA��BD��
(2)��֤��ƽ��BDE��ƽ��PAC��
(3)��PA��ƽ��BDEʱ��������E��BCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sin2x+
sin2x+ ![]() sin2x��
sin2x��
��1������f��x���ĵ����ݼ����䣻
��2���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����f�� ![]() ��=
��= ![]() ����ABC�����Ϊ3
����ABC�����Ϊ3 ![]() ����a����Сֵ��
����a����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����绰������ĵ绰���1��ʱ���ӵĸ�����0.1�����2��ʱ���ӵĸ�����0.2�����3��ʱ���ӵĸ�����0.3�����4��ʱ���ӵĸ�����0.35.
��1������ĵ绰����5��֮ǰ���ӵĸ����Ƕ��٣�
��2������ĵ绰��4���������ӵĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��f��x��=ax2��ex��a��R���� ����a=1ʱ�����ж�f��x���ĵ����Բ�����֤����
������f��x����������ֵ��x1 �� x2��x1��x2����
��i�� ��ʵ��a��ȡֵ��Χ��
��ii��֤������ ![]() �� ��ע��e����Ȼ�����ĵ�����
�� ��ע��e����Ȼ�����ĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���6���ɲ��У���������4�ˣ�Ů��2�ˣ�ѡ3�˲μ�ѧУ�������Ͷ���
��1������ѡ3����Ů������Ϊ�Σ���εķֲ��м�E�Σ�
��2����������Ů���ұ�ѡ�еĸ��ʣ�
��3���������ױ�ѡ�е�����£���Ů����Ҳ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
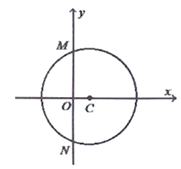
����Ŀ����֪Բ����x���������ϵ�ԲC��ֱ��![]() ���У���y�ύ��M��N���㣬��
���У���y�ύ��M��N���㣬��![]() ��
��
![]() ��
��![]() ��ԲC�ı����̣�
��ԲC�ı����̣�
![]() ��
��![]() ����
����![]() ��ֱ��l��ԲC���ڲ�ͬ������D��E����
��ֱ��l��ԲC���ڲ�ͬ������D��E����![]() ʱ����ֱ��l�ķ��̣�
ʱ����ֱ��l�ķ��̣�
![]() ��
��![]() ��֪Q��ԲC������һ�㣬�ʣ���x�����Ƿ����������A��B��ʹ��
��֪Q��ԲC������һ�㣬�ʣ���x�����Ƿ����������A��B��ʹ��![]() �������ڣ����A��B��������ꣻ�������ڣ���˵�����ɣ�
�������ڣ����A��B��������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com