
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)已知![]() 为
为![]() 的两个零点,证明:
的两个零点,证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】分析:(1)首先确定函数的定义域,之后对函数求导,对参数![]() 进行讨论,当导数大于零时单调增,当导数小于零时单调减;
进行讨论,当导数大于零时单调增,当导数小于零时单调减;
(2)由函数有两个零点,根据第一问的结论,可以断定![]() ,分别将两个零点代入函数解析式,得到两个方程,将两式相减得到
,分别将两个零点代入函数解析式,得到两个方程,将两式相减得到![]() ,即
,即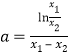 ,之后将问题转化,构造新函数,利用导数研究函数的性质,从而证得结果.
,之后将问题转化,构造新函数,利用导数研究函数的性质,从而证得结果.
详解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时
时![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,
令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减.
上单调递减.
(2)由![]() 为
为![]() 的两个零点及(1)知
的两个零点及(1)知![]() ,
,
∴![]() ,两式相减得
,两式相减得![]() ,即
,即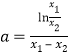 ,
,
要证![]() ,只需证
,只需证![]() ,
,
即证 ,即证
,即证![]()
![]() ,
,
不妨设![]() ,令
,令![]() ,只需证
,只需证![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上单减,
上单减,
∴![]() ,∴
,∴![]() 在
在![]() 上单增,
上单增,
∴![]() ,即
,即![]() 在
在![]() 时恒成立,原不等式得证.
时恒成立,原不等式得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC= ![]() AB,若四面体P﹣ABC的体积为
AB,若四面体P﹣ABC的体积为 ![]() ,则该球的体积为( )
,则该球的体积为( )
A.![]()
B.2π
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示. 
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考) (参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段选取6名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在亚丁湾海域执行护航任务的中国海军“徐州”舰,在A处收到某商船在航行中发出求救信号后,立即测出该商船在方位角方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离A处为10 n mile的C处,并测得该船正沿方位角为105°的方向,以9 n mile/h的速度航行,“徐州”舰立即以21 n mile/h的速度航行前去营救.
(1)“徐州”舰最少需要多少时间才能靠近商船?
(2)在营救时间最少的前提下,“徐州”舰应按照怎样的航行方向前进?(角度精确到0.1°,时间精确到1min,参考数据:sin68.2°≈0.9286)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在(﹣1,+∞)上单调,且函数y=f(x﹣2)的图象关于x=1对称,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
A.﹣200
B.﹣100
C.0
D.﹣50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,b= ![]() sinB,且满足tanA+tanC=
sinB,且满足tanA+tanC= ![]() . (Ⅰ)求角C和边c的大小;
. (Ⅰ)求角C和边c的大小;
(Ⅱ)求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx+x(x﹣a)2(a∈R),若存在 ![]() ,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
,使得f(x)>xf'(x)成立,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=a lnx+![]() +x (a≠0).
+x (a≠0).
(1)若曲线y=f (x)在点(1,f (1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f (x)的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com