
分析 在所给的等式中,令x=1,可得a0+a1+a2+…+a2015 =1 ①,再令x=-1,可得a0-a1+a2+…-a2015 =32015 ②,由①②求得a0+a2+a4+…+a2014 和a1+a3+a5+…+a2015 ,从而求得要求式子的值.
解答 解:∵(2-x)2015=a0+a1x+a2x2+…+a2015x2015,
令x=1,可得a0+a1+a2+…+a2015 =1 ①,
再令x=-1,可得a0-a1+a2+…-a2015 =32015 ②,
由①+②可得a0+a2+a4+…+a2014 =$\frac{1{+3}^{2015}}{2}$,
由①-②可得a1+a3+a5+…+a2015 =$\frac{1{-3}^{2015}}{2}$,
∴$\frac{{a}_{0}+{a}_{2}+{a}_{4}+…+{a}_{2014}}{{a}_{1}+{a}_{3}+{a}_{5}+…+{a}_{2015}}$=$\frac{{1+3}^{2015}}{1{-3}^{2015}}$,
故答案为:$\frac{{1+3}^{2015}}{1{-3}^{2015}}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{2}^{x}-1}$ | B. | y=$\sqrt{5-3x}$ | C. | y=log2(x2+100) | D. | y=3x-100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
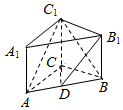 如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.
如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 使用寿命 | [500,700) | [700,900) | [900,1100) | [1100,1300) | [1300,1500] |
| 只数 | 5 | 23 | 44 | 25 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com