
���� �����⻭��ͼ�Σ������12���εı߳�����������ɵã���$\overrightarrow{{A}_{1}{A}_{2}}$��$\overrightarrow{{A}_{2}{A}_{3}}$��$\overrightarrow{{A}_{3}{A}_{4}}$������$\overrightarrow{{A}_{12}{A}_{1}}$��12����������ȡ������ʹ���ǵ�������������������н���С����������Ϊ�������������ɴ˿ɵô𰸣�
��� �⣺��ͼ��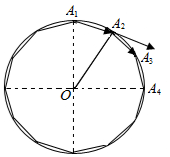
�ɶ�����ڽǺͶ�����֪����12����A1A2��A12�ڽǺ�Ϊ��12-10����180��=1800�㣬
��ÿһ���ڽ�Ϊ$\frac{1800��}{12}=150��$��
��A1OA2=30�㣬
�ڡ�A1OA2�У���OA1=OA2=1��
�����Ҷ����ɵã�$|\overrightarrow{{A}_{1}{A}_{2}}{|}^{2}={1}^{2}+{1}^{2}-2��1��1��cos30��=2-\sqrt{3}$��
�������֪��$\overrightarrow{{A}_{1}{A}_{2}}$��$\overrightarrow{{A}_{2}{A}_{3}}$��$\overrightarrow{{A}_{3}{A}_{4}}$������$\overrightarrow{{A}_{12}{A}_{1}}$��ģ��ȣ�
��$\overrightarrow{{A}_{1}{A}_{2}}$��$\overrightarrow{{A}_{2}{A}_{3}}$��$\overrightarrow{{A}_{3}{A}_{4}}$������$\overrightarrow{{A}_{12}{A}_{1}}$��12����������ȡ������ʹ���ǵ����������
���������н���С����������Ϊ������������
����ȡ$\overrightarrow{{A}_{1}{A}_{2}}$��$\overrightarrow{{A}_{2}{A}_{3}}$��
��S=$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{2}{A}_{3}}=|\overrightarrow{{A}_{1}{A}_{2}}{|}^{2}cos30��$=$��2-\sqrt{3}����\frac{\sqrt{3}}{2}=\sqrt{3}-\frac{3}{2}$��
�ʴ�Ϊ��$\sqrt{3}-\frac{3}{2}$��
���� ���⿼��ƽ�����������������㣬��������������������ͼ������ȷ���������ǽ�����Ĺؼ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 83 | B�� | 63 | C�� | 57 | D�� | 23 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{11}$ | B�� | $\sqrt{10}$ | C�� | 3 | D�� | 2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $10\sqrt{3}$���� | B�� | $\frac{{10\sqrt{6}}}{3}$���� | C�� | $5\sqrt{2}$ ���� | D�� | $5\sqrt{6}$���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com