
| A. | 83 | B. | 63 | C. | 57 | D. | 23 |
分析 直接利用数量积的坐标运算得答案.
解答 解:∵$\overrightarrow a=(-4,3)$,$\overrightarrow b=(5,6)$,
∴$|\overrightarrow{a}|=\sqrt{(-4)^{2}+{3}^{2}}=5$,$\overrightarrow{a}•\overrightarrow{b}=(-4,3)•(5,6)=-4×5+3×6=-2$,
∴$3|\overrightarrow{a}{|}^{2}-4\overrightarrow{a}•\overrightarrow{b}=3×25-4×(-2)=83$.
故选:A.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标表示,是基础题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
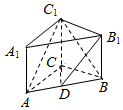 如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.
如图,已知侧棱垂直底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com