
已知向量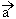 =(
=(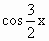 ,
,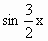 ),
),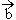 =(
=(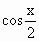 ,-
,-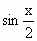 ),且x∈[0,
),且x∈[0,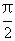 ],求
],求
(1)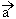 ·
·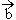 及|
及|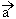 +
+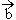 |;
|;
(2)若f(x)=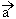 ·
·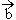 -2λ|
-2λ|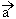 +
+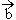 |的最小值是-
|的最小值是-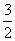 ,求λ的值.
,求λ的值.
|
解:(1) | = ∵x∈[0, (2)f(x)=cos2x-4λcosx,即f(x)=2(cosx-λ)2-1-2λ2 ∵x∈[0, ①当λ<0时,当且仅当cosx=0时,f(x)取得最小值-1,这与已知矛盾; ②当0≤λ≤1时,当且仅当cosx=λ时,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=- ③当λ>1时,当且仅当cosx=1时,f(x)取得最小值1-4λ.由已知得1-4λ=- 解得λ= |


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
已知向量a=(cos![]() x,sin
x,sin![]() x),b=(cos
x),b=(cos![]() ,-sin
,-sin![]() ),且x∈[0,
),且x∈[0,![]() ].求:
].求:
(1)a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知函数f(x)= (a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.
(a、b、c∈N),f(2)=2,f(3)<3且f(x)的图像按向量e=(-1,0)平移后得到的图像关于原点对称.
(Ⅰ)求a,b,c的值;
(Ⅱ)设0<|x|<1,0<|t|≤1,
求证:|t+x|+|t-x|<|f(tx+1)|;
(Ⅲ)设x是正实数,
求证:[f(x+1)]n-f(xn+1)≥2n-2.
查看答案和解析>>
科目:高中数学 来源:湖南省十校联考2007届高三理科数学试题 题型:044
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:广东省普宁市第一中学2006-2007高三第三次周日考试数学(理科)试题 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com