
已知{an}是等差数列,其前n项的和为Sn, {bn}是等比数列,且a1=b1=2,a4+b4=21,
S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
(1)an=n+1,bn=2n,(2)Tn=n·2n+1
【解析】
试题分析:(1)求等差数列及等比数列通项公式,通常利用待定系数法求解. 设等差数列{an}的公差为d,等比数列{bn}的公比为q.由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d.由条件a4+b4=21,S4+b4=30,得方程组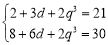 解得
解得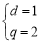 .所以an=n+1,bn=2n,n∈N*.(2)数列{cn}是等差乘等比型,因此其和用错位相减法求. 记Tn=c1+c2+c3+ +cn.2 Tn=2×22+3×23+ +(n-1)×2n-1+n×2n+ (n+1)2n+1,所以-Tn=2×2+(22+23+ +2n )-(n+1)×2n+1,即Tn=n·2n+1,n∈N*.
.所以an=n+1,bn=2n,n∈N*.(2)数列{cn}是等差乘等比型,因此其和用错位相减法求. 记Tn=c1+c2+c3+ +cn.2 Tn=2×22+3×23+ +(n-1)×2n-1+n×2n+ (n+1)2n+1,所以-Tn=2×2+(22+23+ +2n )-(n+1)×2n+1,即Tn=n·2n+1,n∈N*.
试题解析:【解析】
(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.
由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d. 3分
由条件a4+b4=21,S4+b4=30,得方程组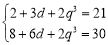 解得
解得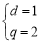
所以an=n+1,bn=2n,n∈N*. 7分
(2)由题意知,cn=(n+1)×2n.
记Tn=c1+c2+c3+ +cn.
则Tn=c1+c2+c3+ +cn
=2×2+3×22+4×23+ +n×2n-1 +(n+1)×2n,
2 Tn= 2×22+3×23+ +(n-1)×2n-1+n×2n+ (n+1)2n+1,
所以-Tn=2×2+(22+23+ +2n )-(n+1)×2n+1, 11分
即Tn=n·2n+1,n∈N*. 14分
考点:等差数列及等比数列通项公式,错位相减法求和


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源:2015届江苏省高二第二学期阶段测试文科数学试卷(解析版) 题型:解答题
已知命题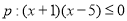 ,命题
,命题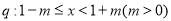 。
。
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“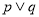 ”为真命题,“
”为真命题,“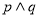 ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
设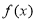 使定义在区间
使定义在区间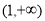 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数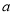 和函数
和函数 ,其中
,其中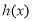 对任意的
对任意的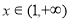 都有
都有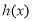 >0,使得
>0,使得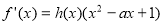 ,则称函数
,则称函数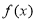 具有性质
具有性质 .
.
(1)设函数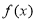
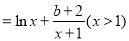 ,其中
,其中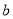 为实数
为实数
①求证:函数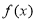 具有性质
具有性质 ,②求函数
,②求函数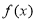 的单调区间.
的单调区间.
(2)已知函数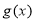 具有性质
具有性质 ,给定
,给定
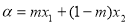 ,
,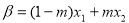 ,且
,且 ,若|
,若|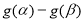 |<|
|<|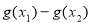 |,求
|,求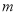 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
已知矩阵A= 属于特征值?的一个特征向量为α=
属于特征值?的一个特征向量为α= .
.
(1)求实数b,?的值;
(2)若曲线C在矩阵A对应的变换作用下,得到的曲线为C?:x2+2y2=2,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:填空题
记数列{an}的前n项和为Sn.若a1=1,Sn=2(a1+an)(n≥2,n∈N*),则Sn= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com