
设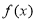 使定义在区间
使定义在区间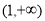 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数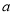 和函数
和函数 ,其中
,其中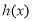 对任意的
对任意的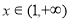 都有
都有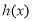 >0,使得
>0,使得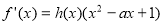 ,则称函数
,则称函数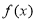 具有性质
具有性质 .
.
(1)设函数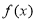
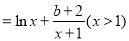 ,其中
,其中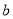 为实数
为实数
①求证:函数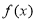 具有性质
具有性质 ,②求函数
,②求函数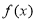 的单调区间.
的单调区间.
(2)已知函数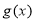 具有性质
具有性质 ,给定
,给定
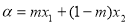 ,
,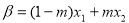 ,且
,且 ,若|
,若|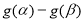 |<|
|<|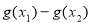 |,求
|,求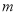 的取值范围.
的取值范围.
(1)①祥见解析;②当b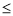 2时,
2时, 在区间(1,+∞)上递增;
在区间(1,+∞)上递增;
当b>2时, 在(1,
在(1, )上递减;
)上递减; 在[
在[ ,+∞)上递增.
,+∞)上递增.
(2)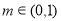 .
.
【解析】
试题分析:(1)①先求出函数 的导函数
的导函数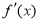 ,然后将其配凑成
,然后将其配凑成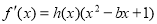 这种形式,再说明h(x)对任意的x∈(1,+
这种形式,再说明h(x)对任意的x∈(1,+ )都有h(x)>0,即可证明函数
)都有h(x)>0,即可证明函数 具有性质P(b);
具有性质P(b);
②根据第一问令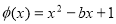 ,讨论对称轴与2的大小,当b
,讨论对称轴与2的大小,当b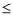 2时,对于x>1,
2时,对于x>1,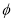 (x)>0,所以
(x)>0,所以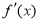 >0,可得
>0,可得 在区间(1,+
在区间(1,+ )上单调性,当b>2时,
)上单调性,当b>2时,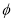 (x)图象开口向上,对称轴
(x)图象开口向上,对称轴 ,可求出方程
,可求出方程 (x)=0的两根,判定两根的范围,从而确定
(x)=0的两根,判定两根的范围,从而确定 (x)的符号,得到
(x)的符号,得到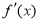 的符号,最终求出单调区间.
的符号,最终求出单调区间.
(2)由题设知,函数g(x)得导数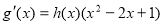 ,其中h(x)>0对于任意得x
,其中h(x)>0对于任意得x (1,+
(1,+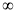 )都成立,当x>1时,
)都成立,当x>1时,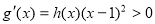 ,从而g(x)在(1,+
,从而g(x)在(1,+ )上单调递增,分
)上单调递增,分
①m (0,1)②m
(0,1)②m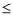 0③m
0③m 1三种情况讨论求解m得范围即可.
1三种情况讨论求解m得范围即可.
试题解析:(1)①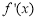
 ∵
∵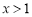 时,
时,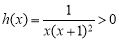 恒成立,∴函数
恒成立,∴函数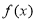 具有性质
具有性质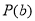 ;
;
②当b≤2时,对于x>1,
所以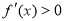 ,故此时
,故此时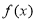 在区间(1,+∞)上递增;
在区间(1,+∞)上递增;
当b>2时, (x)图象开口向上,对称轴
(x)图象开口向上,对称轴 ,
,
方程 的两根为:
的两根为: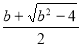 ,
,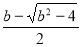
而  >1,
>1,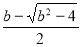

当 x∈(1, )时,
)时, ,
,
故此时 在区间 (1,
在区间 (1, )上递减;
)上递减;
同理得: 在区间[
在区间[ ,+
,+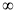 )上递增.
)上递增.
综上所述,当b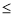 2时,
2时, 在区间(1,+
在区间(1,+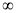 )上递增;
)上递增;
当b>2时, 在 (1,
在 (1, )上递减;
)上递减; 在[
在[ ,+∞)上递增.
,+∞)上递增.
(2)由题设知,函数 得导数
得导数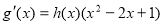 ,其中h(x)>0对于任意得x
,其中h(x)>0对于任意得x (1,+
(1,+ )都成立
)都成立
 当x>1时,
当x>1时,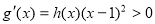 ,从而
,从而 在(1,+
在(1,+ )上单调递增
)上单调递增
①当m (0,1),
(0,1), ,且
,且
∴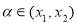 ;同理可得
;同理可得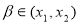
由 的单调性可知,
的单调性可知,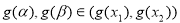
从而有 符合题意
符合题意
②当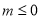 时,
时,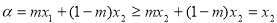
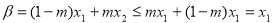 β=(1-m)x1+mx2
β=(1-m)x1+mx2 (1-m)x1+mx1=mx1
(1-m)x1+mx1=mx1
于是由 及
及 的单调性可知
的单调性可知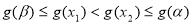
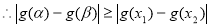 与题设不符,
与题设不符,
③当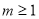 时,同理可得
时,同理可得 ,进而可得
,进而可得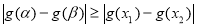 与题设不符;
与题设不符;
综合①②③可得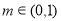
考点:1.比较大小;2.利用导数研究函数的单调性.


科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
已知{an}是等差数列,其前n项的和为Sn, {bn}是等比数列,且a1=b1=2,a4+b4=21,
S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:解答题
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:

(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com