
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:

(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
(1) ;(2)
;(2)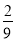 .
.
【解析】
试题分析:(1)利用分步乘法原理即可得出涂完三个矩形共有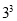 种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即
种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即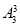 种涂法.利用古典概型的概率计算公式即可得出.
种涂法.利用古典概型的概率计算公式即可得出.
试题解析:(1)由题意可知:用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,可以分三步去完成:
涂第一个矩形可有三种方法,涂第二个矩形可有三种方法,涂第三个矩形可有三种方法,
由分步乘法原理可得涂完三个矩形共有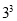 =27种方法,其中3个矩形都涂同一颜色的方法只有三种.
=27种方法,其中3个矩形都涂同一颜色的方法只有三种.
设“3个矩形都涂同一颜色”为事件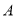 ,则
,则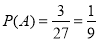 .
.
(2)由(1)可知:三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,方法共有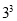 .
.
设“3个小矩形颜色都不同”为事件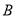 ,则事件
,则事件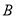 包括
包括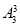 种涂法.
种涂法.
由古典概型的概率计算公式可得: .
.
考点:1、古典概型的概率;2、排列的应用.


科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
设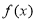 使定义在区间
使定义在区间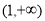 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数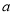 和函数
和函数 ,其中
,其中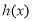 对任意的
对任意的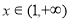 都有
都有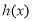 >0,使得
>0,使得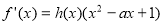 ,则称函数
,则称函数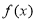 具有性质
具有性质 .
.
(1)设函数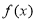
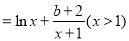 ,其中
,其中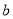 为实数
为实数
①求证:函数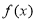 具有性质
具有性质 ,②求函数
,②求函数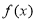 的单调区间.
的单调区间.
(2)已知函数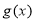 具有性质
具有性质 ,给定
,给定
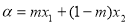 ,
,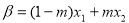 ,且
,且 ,若|
,若|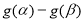 |<|
|<|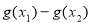 |,求
|,求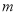 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
有在外观上没有区别的5件产品,其中3件合格,2件不合格,从中任意抽检2件,则至少有一件不合格的概率为___________.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
“ ”是“
”是“ ”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)
”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com