
科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数 ,
,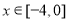 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧. ⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧. ⑴试确定A,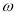 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设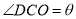 (弧度),试用
(弧度),试用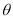 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)

查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二第二学期阶段测试文科数学试卷(解析版) 题型:解答题
已知命题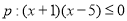 ,命题
,命题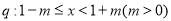 。
。
(1)若p是q的充分条件,求实数m的取值范围;
(2)若m=5,“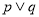 ”为真命题,“
”为真命题,“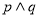 ”为假命题,求实数x的取值范围。
”为假命题,求实数x的取值范围。
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:解答题
函数 在
在 时取得极小值.
时取得极小值.
(1)求实数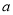 的值;
的值;
(2)是否存在区间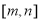 ,使得
,使得 在该区间上的值域为
在该区间上的值域为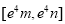 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:填空题
求“方程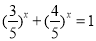 的解”有如下解题思路:设
的解”有如下解题思路:设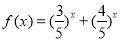 ,则
,则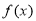 在
在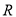 上单调递减,且
上单调递减,且 ,所以原方程有唯一解
,所以原方程有唯一解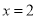 .类比上述解题思路,方程
.类比上述解题思路,方程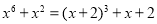 的解集为_ __ .
的解集为_ __ .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
设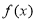 使定义在区间
使定义在区间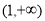 上的函数,其导函数为
上的函数,其导函数为 .如果存在实数
.如果存在实数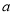 和函数
和函数 ,其中
,其中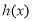 对任意的
对任意的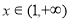 都有
都有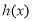 >0,使得
>0,使得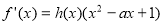 ,则称函数
,则称函数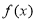 具有性质
具有性质 .
.
(1)设函数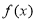
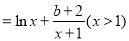 ,其中
,其中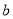 为实数
为实数
①求证:函数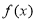 具有性质
具有性质 ,②求函数
,②求函数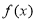 的单调区间.
的单调区间.
(2)已知函数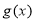 具有性质
具有性质 ,给定
,给定
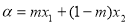 ,
,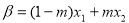 ,且
,且 ,若|
,若|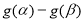 |<|
|<|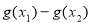 |,求
|,求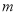 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com