
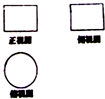
 如图所示的是一个立体图形的三视图,此立体图形的名称为:
如图所示的是一个立体图形的三视图,此立体图形的名称为:科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 种子处理 | 种子未处理 | 总计 | |
| 得病 | 32 | 101 | 133 |
| 不得病 | 61 | 213 | 274 |
| 总计 | 93 | 314 | 407 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、回归分析中,相关指数R2的值越大,说明残差平方和越小 |
| B、若一组观测值(x1,y1),(x2,y2),…,(xn,yn)满足yi=bxi+a+ei(i=1,2,…,n),若ei恒为0,则R2=1 |
| C、回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法 |
| D、画残差图时,纵坐标为残差,横坐标一定是编号 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com