Question

19．非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow a$的夹角为$\frac{π}{6}$，向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow b$的夹角为$\frac{π}{4}$则$\frac{|\overrightarrow a|}{|\overrightarrow b|}$等于$\sqrt{2}$．

Answer 1

分析 根据题意画出?ABCD，设$\overrightarrow{AB}=\overrightarrow{a}$、$\overrightarrow{AD}=\overrightarrow{b}$，根据平行四边形法则求出$\overrightarrow{a}+\overrightarrow{b}$，由题意求出∠DAC、∠CAB和∠ACD，利用正弦定理求出$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$的值．

解答 解：由题意画出?ABCD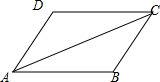，设$\overrightarrow{AB}=\overrightarrow{a}$，$\overrightarrow{AD}=\overrightarrow{b}$，则$\overrightarrow{a}+\overrightarrow{b}$=$\overrightarrow{AC}$，
∵向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow a$的夹角为$\frac{π}{4}$，向量$\overrightarrow{a}$+$\overrightarrow{b}$与向量$\overrightarrow b$的夹角为$\frac{π}{4}$，
∴∠DAC=$\frac{π}{4}$，∠CAB=$\frac{π}{6}$，则∠ACD=$\frac{π}{6}$，
在△ADC中，由正弦定理得$\frac{CD}{sin∠DAC}=\frac{AD}{sin∠ACD}$，
∴$\frac{CD}{AD}=\frac{sin∠DAC}{sin∠ACD}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=$\sqrt{2}$，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}$=$\sqrt{2}$，
故答案为：$\sqrt{2}$．

点评 本题考查向量的加法法则，以及其几何意义，以及正弦定理的应用，考查数形结合思想．