练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．函数y=2x-1的值域是（　　）
    A．（-∞，1）B．（-∞，0）∪（0，+∞）C．（-1，+∞）D．（-∞，-1）∪（0，+∞）

    分析 根据指数函数的值域可得函数y=2x-1的值域．

    解答 解：∵y=2x的值域为（0，+∞），
    那么：函数y=2x-1的值域为（-1，+∞）．
    故选：C．

    点评 本题考查了函数值域的求法．高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法．要根据题意选择．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．若集合A={-1，0，1，2，3}，B={y|y=2x-1，x∈A}，集合C=A∩B，则C的真子集个数为（　　）
    A．3B．4C．7D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

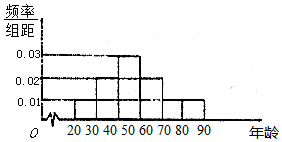    5．退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势，某机构为了解某城市市民的年龄构成，从该城市市民中随机抽取年龄段在20～80岁（含20岁和80岁）之间的600人进行调查，并按年龄层次绘制频率分布直方图，如图所示，若规定年龄分布在60～80岁（含60岁和80岁）为“老年人”．
    （1）若每一组数据的平均值用该区间中点值来代替，可估算所调查的600人的平均年龄；
    （2）依据直方图计算所调查的600人年龄的中位数（结果保留一位小数）；
    （3）如果规定：年龄在20～40岁为青年人，在41～59岁为中年人，为了了解青年、中年、老年人对退休年龄延迟的态度，特意从这600人重随机抽取n人进行座谈，若从中年人中抽取了10人，试问抽取的座谈人数是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知集合A={-1，0，1}，B={x|x=sin$\frac{2k+1}{2}$π，k∈Z}，则∁AB=（　　）
    A．?B．0C．{0}D．{-1，1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．某三棱锥的三视图如图所示，该三棱锥的体积是（　　）
    A．$\frac{4}{3}$B．$\frac{8}{3}$C．4D．$6+2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知集合A={x|x2-3x+2＜0}，B={x|y=lg（3-x）}，则A∩B=（　　）
    A．{x|1＜x＜2}B．{x|1＜x＜3}C．{x|2＜x＜3}D．{x|x＜3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

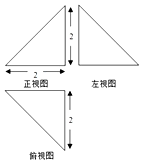
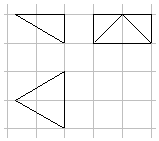    6．如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，已知其俯视图是正三角形，则该四棱锥的外接球的表面积是（　　）
    A．$\frac{19π}{3}$B．$\frac{22π}{3}$C．19πD．22π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．近年来，我国电子商务蓬勃发展.2016年“618”期间，某网购平台的销售业绩高达516亿元人民币，与此同时，相关管理部门推出了针对该网购平台的商品和服务的评价系统．从该评价系统中选出200次成功交易，并对其评价进行统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的交易为80次．
    （Ⅰ） 根据已知条件完成下面的2×2列联表，并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”？
    对服务满意对服务不满意合计
    对商品满意80
    对商品不满意
    合计200
    （Ⅱ） 若将频率视为概率，某人在该网购平台上进行的3次购物中，设对商品和服务都满
    意的次数为随机变量X，求X的分布列和数学期望EX．
    附：K2=$\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
    P（K2≥k）0.150.100.050.0250.010
    k2.0722.7063.8415.0246.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知函数y=f（x）（x∈R）的图象过点（1，0），f'（x）是函数f（x）的导函数，e为自然对数的底数，若x＞0时，xf'（x）＞1恒成立，则不等式f（x）≤lnx的解集是（0，1]．

    查看答案和解析>>

    同步练习册答案