练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】双曲线 的左、右焦点分别为，过作倾斜角为的直线与轴和双曲线的右支分别交于两点，若点平分线段，则该双曲线的离心率是（ ）

    A. B. C. 2 D.

    【答案】B

    【解析】双曲线 的左焦点为,直线的方程为，令，则，即，因为平分线段，根据中点坐标公式可得 ，代入双曲线方程，可得，由于，则，化简可得，解得，由，解得，故选B.

    【方法点晴】本题主要考查利用双曲线的简单性质求双曲线的离心率，属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析，既使不画出图形，思考时也要联想到图形，当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系.求离心率问题应先将 用有关的一些量表示出来，再利用其中的一些关系构造出关于的等式，从而求出的值.本题是利用点到直线的距离等于圆半径构造出关于的等式，最后解出的值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆（），圆（），若圆的一条切线与椭圆相交于两点.

    （1）当， 时，若点都在坐标轴的正半轴上，求椭圆的方程；

    （2）若以为直径的圆经过坐标原点，探究是否满足，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）如图，在多面体中， 是正方形， 平面, 平面, ,点为棱的中点.

    （1）求证：平面平面；

    （2）若,求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙二人约定某日早上在某处会面，甲在内某一时刻随机到达，乙在内某一时刻随机到达，则甲至少需等待乙5分钟的概率是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代十进制的算筹计数法，在世界数学史上是一个伟大的创造，算筹实际上是一根根同样长短的小木棍，如图，算筹表示数1～9的方法的一种.

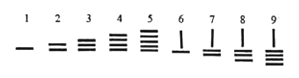
    例如：163可表示为“”27可表示为“”问现有8根算筹可以表示三位数的个数（算筹不能剩余）为（ ）

    A. 48 B. 60 C. 96 D. 120

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）求函数的最小正周期；

    （2）常数，若函数在区间上是增函数，求的取值范围；

    （3）若函数在的最大值为2，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.一个人打靶，打了10发子弹，有7发子弹中靶，因此这个人中靶的概率为

    B.某地发行福利彩票，其回报率为，有个人花了100元钱买彩票，一定会有47元回报

    C.根据最小二乘法求得的回归直线一定经过样本中心点

    D.大量试验后，可以用频率近似估计概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定集合（且），定义点集，若对任意点，存在,使得 (为坐标原点）.则称集合具有性质，给出一下四个结论：

    ①其有性质；

    ②具有性质；

    ③若集合具有性质，则中一定存在两数，使得；

    ④若集合具有性质.是中任一数，则在中一定存在，使得.

    其中正确结论有___________(填上你认为所有正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】是偶函数，

    (1) 求的值；

    (2)当时，设，若函数与的图象有且只有一个公共点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案