
【题目】下列说法正确的是( )
A.一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为![]()
B.某地发行福利彩票,其回报率为![]() ,有个人花了100元钱买彩票,一定会有47元回报
,有个人花了100元钱买彩票,一定会有47元回报
C.根据最小二乘法求得的回归直线![]() 一定经过样本中心点
一定经过样本中心点![]()
D.大量试验后,可以用频率近似估计概率.
科目:高中数学 来源: 题型:
【题目】下列命题中,其中错误命题有( )
A.单位向量都相等
B.在![]() 中,若
中,若![]() ,则
,则![]() 一定大于
一定大于![]() ;
;
C.若数列![]() 的前
的前![]() 项和为
项和为![]() (
(![]() 、
、![]() 、
、![]() 均为常数),则数列
均为常数),则数列![]() 一定为等差数列;
一定为等差数列;
D.若数列![]() 是等比数列,则数列
是等比数列,则数列![]() 也是等比数列
也是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]()
![]() 的两个焦点为
的两个焦点为![]() ,点P在椭圆C 上,且
,点P在椭圆C 上,且 ![]() ,
,![]() ,
,![]() .
.
(1)求椭圆C的方程;
(2)若直线L过点![]() 交椭圆于A、B两点,且点M为线段AB的中点,求直线L的一般方程.
交椭圆于A、B两点,且点M为线段AB的中点,求直线L的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 作倾斜角为
作倾斜角为![]() 的直线与
的直线与![]() 轴和双曲线的右支分别交于
轴和双曲线的右支分别交于![]() 两点,若点
两点,若点![]() 平分线段
平分线段![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
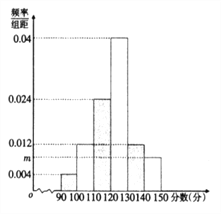
(1)求![]() 的值及这50名同学数学成绩的平均数
的值及这50名同学数学成绩的平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,若已知成在
的同学中选出3位作为代表进行座谈,若已知成在![]() 的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,它的制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。某陶瓷厂准备仿制甲、乙、丙三件不同的唐三彩工艺品,根据该厂全面治污后的技术水平,经过第一次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() ,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次烧制后甲、乙、丙三件中恰有一件工艺品合格的概率;
(2)经过前后两次烧制后,甲、乙、丙三件工艺品成为合格工艺品的件数为![]() ,求随机变量
,求随机变量![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南京江北新区是第十三个国家级新区,随着新区的经济发展,老城区将不断的进行开发和改造,如图为边长为4km的正三角形![]() 区域,
区域,![]() 分别在三边
分别在三边![]() 上,且
上,且![]() 为
为![]() 的中点,
的中点,![]() ,现将对正三角形
,现将对正三角形![]() 区域进行规划,规划
区域进行规划,规划![]() 区域为娱乐广场,其他区域为生活居住区.
区域为娱乐广场,其他区域为生活居住区.
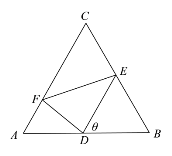
(1)若![]() ,求娱乐广场
,求娱乐广场![]() 的面积;
的面积;
(2)求生活区域的面积![]() 的最大值,并写出
的最大值,并写出![]() 取得最大值时
取得最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两人进行一局围棋比赛,A获得的概率为0.8,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计B获胜的概率.先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5,6,7表示A获胜;8,9表示B获胜,这样能体现A获胜的概率为0.8.因为采用三局两胜制,所以每3个随机数作为一组.
例如,产生30组随机数:034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751,据此估计B获胜的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1) 取出的两球1个是白球,另1个是红球;
(2) 取出的两球至少一个是白球。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com