【题目】对任意等比数列{an}，下列说法一定正确的是（ ）
A.a1 ， a3 ， a9成等比数列
B.a2 ， a3 ， a6成等比数列
C.a2 ， a4 ， a8成等比数列
D.a3 ， a6 ， a9成等比数列
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案科目：高中数学 来源： 题型：
【题目】下列推理过程不是演绎推理的是（ ）．
①一切奇数都不能被2整除，2019是奇数， 2019不能被2整除；
②由“正方形面积为边长的平方”得到结论：正方体的体积为棱长的立方；
③在数列
中，
，
，由此归纳出的通项公式；
④由“三角形内角和为
”得到结论：直角三角形内角和为 .
A. ① ② B. ② ③ C. ③ ④ D. ②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了防止受到核污染的产品影响民众的身体健康，某地要求这种产品在进入市场前必须进行两轮苛刻的核辐射检测，只有两轮检测都合格才能上市销售，否则不能销售。已知该产品第一轮检测不合格的概率为
，第二轮检测不合格的概率为
，每轮检测结果只有“合格”、“不合格”两种，且两轮检测是否合格相互之间没有影响。
（1）求该产品不能上市销售的概率；
（2）如果这种产品可以上市销售，则每件产品可获利50元；如果这种产品不能上市销售，则每件产品亏损80元（即获利为
80元）。现有这种产品4件，记这4件产品获利的金额为
元，求的分布列。
查看答案和解析>>
科目：高中数学 来源： 题型：
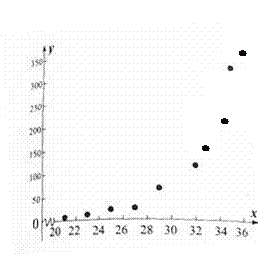
【题目】经观测，某昆虫的产卵数y与温度x有关，现将收集到的温度xi和产卵数yi（i=1，2，…，10）的10组观测数据作了初步处理，得到如下图的散点图及一些统计量表．
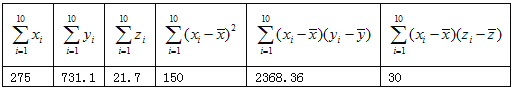
表中
, 
（1）根据散点图判断， 
, 
与
哪一个适宜作为y与x之间的回归方程模型？（给出判断即可，不必说明理由）
（2）根据（1）的判断结果及表中数据．
①试求y关于x回归方程；
②已知用人工培养该昆虫的成本h（x）与温度x和产卵数y的关系为h（x）=x（lny﹣2.4）+170，当温度x（x取整数）为何值时，培养成本的预报值最小？
附：对于一组数据（u1，v1），（u2，v2），…（un，vn），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β=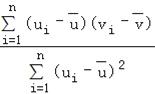
，α=
﹣β
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某市准备在道路
的一侧修建一条运动比赛道，赛道的前一部分为曲线段
，该曲线段是函数
， 
时的图象，且图象的最高点为
.赛道的中间部分为长
千米的直线跑道
，且
.赛道的后一部分是以
为圆心的一段圆弧
.
(1)求
的值和
的大小；
(2)若要在圆弧赛道所对应的扇形
区域内建一个“矩形草坪”，矩形的一边在道路上，一个顶点在半径
上，另外一个顶点
在圆弧上，且
,求当“矩形草坪”的面积取最大值时
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以直角坐标系的原点
为极点， 
轴正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线
的参数方程为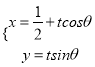
，（ 
为参数， 
），曲线
的极坐标方程为
.
（1）求曲线
的直角坐标方程；
（2）设直线
与曲线
相交于
， 
两点，当
变化时，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
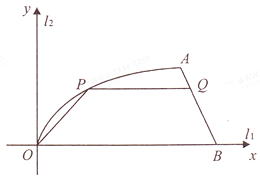
【题目】如图，某小区内有两条互相垂直的道路
与
，平面直角坐标系
的第一象限有一块空地
，其边界是函数
的图象，前一段曲线
是函数
图象的一部分，后一段
是一条线段.测得
到的距离为8米，到的距离为16米，
长为20米.
（1）求函数的解析式；
（2）现要在此地建一个社区活动中心，平面图为梯形
（其中
，为两底边），问：梯形的高为多少米时，该社区活动中心的占地面积最大，并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
