
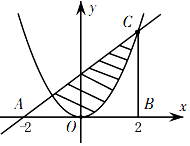
 如图,△ABC中的阴影部分是由曲线y=x2与直线x-y+2=0所围成,向△ABC内随机投掷一点,则该点落在阴影部分的概率为( )
如图,△ABC中的阴影部分是由曲线y=x2与直线x-y+2=0所围成,向△ABC内随机投掷一点,则该点落在阴影部分的概率为( )| A. | $\frac{7}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{7}{16}$ | D. | $\frac{9}{16}$ |
分析 首先分别计算三角形和阴影部分的面积,利用几何概型的公式解答.
解答 解:由题意,△ABC中的面积为$\frac{1}{2}×4×4$=8,△ABC中的阴影部分面积为${∫}_{-1}^{2}(x+2-{x}^{2})dx$=($\frac{1}{2}{x}^{2}+2x-\frac{1}{3}{x}^{3}$)|${\;}_{-1}^{2}$=$\frac{9}{2}$,由几何概型的概率公式得到$\frac{\frac{9}{2}}{8}=\frac{9}{16}$;
故选:D.
点评 本题考查了利用定积分计算曲边梯形的面积以及几何概型的概率求法;正确计算阴影部分的面积是解答的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | 西安中学的年轻老师 | |
| B. | 北师大版高中数学必修一课本上所有的简单题 | |
| C. | 全国所有美丽的城市 | |
| D. | 2016年西安市所有的高一学生 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,$\frac{7}{4}$] | B. | [-$\frac{5}{2}$,-1] | C. | [0,$\sqrt{2}$] | D. | [-1,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com