
 (1)如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=\sqrt{3}\overrightarrow{BD},|\overrightarrow{AD}|=1$,求$\overrightarrow{AC}•\overrightarrow{AD}$的值
(1)如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}=\sqrt{3}\overrightarrow{BD},|\overrightarrow{AD}|=1$,求$\overrightarrow{AC}•\overrightarrow{AD}$的值分析 (1)根据平面向量数量积的定义,利用三角恒等变换与正弦定理,即可求出$\overrightarrow{AC}$•$\overrightarrow{AD}$的值.
(2)解法一:根据题意,利用解析法求解,以直线DA,DC分别为x,y轴建立平面直角坐标系,写出点A、B、C和D的坐标,设出点P,根据向量模的计算公式,利用完全平方式非负,即可求得其最小值;
解法二:设$\overrightarrow{DP}$=x$\overrightarrow{DC}$,得$\overrightarrow{PC}$=(1-x)$\overrightarrow{DC}$,表示出$\overrightarrow{PA}$、$\overrightarrow{PB}$,计算($\overrightarrow{PA}$+3$\overrightarrow{PB}$)2的最小值即可求出|$\overrightarrow{PA}$+3$\overrightarrow{PB}$|的最小值.
解答 解:(1)$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|×|$\overrightarrow{AD}$|×cos∠∠CAD,
∵|$\overrightarrow{AD}$|=1,
∴$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|×cos∠CAD,
∵∠BAC=$\frac{π}{2}$+∠DAC,
∴cos∠CAD=sin∠BAC,
∴$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|sin∠BAC,
在△ABC中,由正弦定理得$\frac{AC}{sinB}$=$\frac{BC}{sin∠BAC}$,
变形得|AC|sin∠BAC=|BC|sinB,
∴$\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|sin∠BAC=|BC|sinB=|BC|•$\frac{AD}{BD}$=$\sqrt{3}$BD•$\frac{AD}{BD}$=$\sqrt{3}$;
(2)解法一:如图,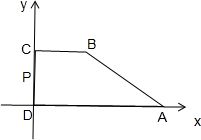 以直线DA,DC分别为x,y轴建立平面直角坐标系,
以直线DA,DC分别为x,y轴建立平面直角坐标系,
则A(2,0),B(1,a),C(0,a),D(0,0)
设P(0,b)(0≤b≤a)
则$\overrightarrow{PA}$=(2,-b),$\overrightarrow{PB}$=(1,a-b),
∴$\overrightarrow{PA}$+3$\overrightarrow{PB}$=(5,3a-4b),
∴|$\overrightarrow{PA}$+3$\overrightarrow{PB}$|=$\sqrt{{5}^{2}{+(3a-4b)}^{2}}$≥5,
即当3a=4b时,取得最小值5;
解法二:直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=1,
$\overrightarrow{CB}$⊥$\overrightarrow{CD}$,$\overrightarrow{DA}$⊥$\overrightarrow{CD}$,$\overrightarrow{DA}$∥$\overrightarrow{CB}$,
设$\overrightarrow{DP}$=x$\overrightarrow{DC}$,则$\overrightarrow{PC}$=(1-x)$\overrightarrow{DC}$,
∴$\overrightarrow{PA}$=$\overrightarrow{DA}$-$\overrightarrow{DP}$=$\overrightarrow{DA}$-x$\overrightarrow{DC}$,$\overrightarrow{PB}$=$\overrightarrow{PC}$+$\overrightarrow{CB}$=(1-x)$\overrightarrow{DC}$+$\overrightarrow{CB}$,
∴($\overrightarrow{PA}$+3$\overrightarrow{PB}$)2=[$\overrightarrow{DA}$+3$\overrightarrow{CB}$+(3-4x)$\overrightarrow{DC}$]2
=${\overrightarrow{DA}}^{2}$+9${\overrightarrow{CB}}^{2}$+(3-4x)2${\overrightarrow{DC}}^{2}$+6$\overrightarrow{DA}$•$\overrightarrow{CB}$+2(3-4x)$\overrightarrow{DA}$•$\overrightarrow{DC}$+6(3-4x)$\overrightarrow{CB}$•$\overrightarrow{DC}$,
∵$\overrightarrow{DA}$•$\overrightarrow{CB}$=2,$\overrightarrow{DA}$•$\overrightarrow{DC}$=$\overrightarrow{CB}$•$\overrightarrow{DC}$=0,
∴($\overrightarrow{PA}$+3$\overrightarrow{PB}$)2=25+(3-4x)2${\overrightarrow{DC}}^{2}$,
当3-4x=0时,($\overrightarrow{PA}$+3$\overrightarrow{PB}$)2min=25,
∴|$\overrightarrow{PA}$+3$\overrightarrow{PB}$|min=5.
点评 本题考查了平面向量的数量积的定义与性质的应用问题,也考查了诱导公式和正弦定理的运用问题,也考查了一题多解的问题,是综合性题目.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | -$\frac{7}{8}$ | D. | -$\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
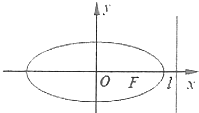 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点到直线$l:x=\frac{a^2}{c}$的距离为$\frac{4\sqrt{5}}{5}$,离心率$e=\frac{{\sqrt{5}}}{3}$,A,B是椭圆上的两动点,动点P满足$\overrightarrow{OP}=\overrightarrow{OA}+λ\overrightarrow{OB}$,(其中λ为常数).
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点到直线$l:x=\frac{a^2}{c}$的距离为$\frac{4\sqrt{5}}{5}$,离心率$e=\frac{{\sqrt{5}}}{3}$,A,B是椭圆上的两动点,动点P满足$\overrightarrow{OP}=\overrightarrow{OA}+λ\overrightarrow{OB}$,(其中λ为常数).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$-$\frac{1}{2}$ | B. | $\frac{π}{4}$+$\frac{1}{2}$ | C. | $\frac{1}{2}$-$\frac{π}{4}$ | D. | $\frac{π}{2}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com