
| A. | $\frac{4}{39}$ | B. | $\frac{7}{78}$ | C. | $\frac{7}{76}$ | D. | $\frac{5}{81}$ |
分析 根据题意将毎等人所得的黄金斤数构造等差数列,设公差为d,根据题意和等差数列的前n项和公式列出方程组,求出公差d即可得到答案.
解答 解:设第十等人得金a1斤,第九等人得金a2斤,以此类推,第一等人得金a10斤,
则数列{an}构成等差数列,设公差为d,则每一等人比下一等人多得d斤金,
由题意得$\left\{\begin{array}{l}{{a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}=3}\\{{a}_{8}+{a}_{9}+{a}_{10}=4}\end{array}\right.$,即$\left\{\begin{array}{l}{4{a}_{1}+6d=3}\\{3{a}_{1}+24d=4}\end{array}\right.$,
解得d=$\frac{7}{78}$,
∴每一等人比下一等人多得$\frac{7}{78}$斤金.
故选:B.
点评 本题考查等差数列的定义,前n项和公式在实际问题中的应用,以及方程思想,是基础题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | y=ln(x2+1) | B. | y=cosx | C. | y=x-lnx | D. | y=($\frac{1}{2}$)|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | 4 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
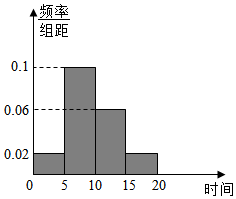 某市为了缓解交通压力,提倡低碳环保,鼓励市民乘坐公共交通系统出行.为了更好地保障市民出行,合理安排运力,有效利用公共交通资源合理调度,在某地铁站点进行试点调研市民对候车时间的等待时间(候车时间不能超过20分钟),以便合理调度减少候车时间,使市民更喜欢选择公共交通.为此在该地铁站的一些乘客中进行调查分析,得到如下统计表和各时间段人数频率分布直方图:
某市为了缓解交通压力,提倡低碳环保,鼓励市民乘坐公共交通系统出行.为了更好地保障市民出行,合理安排运力,有效利用公共交通资源合理调度,在某地铁站点进行试点调研市民对候车时间的等待时间(候车时间不能超过20分钟),以便合理调度减少候车时间,使市民更喜欢选择公共交通.为此在该地铁站的一些乘客中进行调查分析,得到如下统计表和各时间段人数频率分布直方图:| 分组 | 等待时间(分钟) | 人数 |
| 第一组 | [0,5) | 10 |
| 第二组 | [5,10) | a |
| 第三组 | [10,15) | 30 |
| 第四组 | [15,20) | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{8π}{3}$ | D. | 3π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com