
| φ |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| ωx |
| 2 |
| 5π |
| 12 |
| 1 |
| 2 |
| φ |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 7π |
| 6 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
| ωx |
| 2 |
| 5π |
| 12 |
| (|sinωx|+|cosωx|)2 |
| 1+|sin2ωx| |
| π |
| 2ω |
| π |
| 2ω |
| π |
| 4ω |
| π |
| 2ω |
| π |
| 4ω |
| 99π |
| 4 |
| 101π |
| 4 |


科目:高中数学 来源: 题型:
| a |
| i |
| j |
| a |
| b |
| i |
| j |
| i |
| j |
| a |
| b |
| p |
| q |
| p |
| q |
| 0 |
| p |
| q |
| p |
| q |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
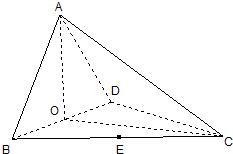 如图,四面体ABCD中,O、E分别是BD、BC的中点,AB=AD=
如图,四面体ABCD中,O、E分别是BD、BC的中点,AB=AD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.| x | 3 | 4 | 5 | 6 |
| t | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com