( 本题满分12分) 已知函数
(1)求
的最小正周期、单调增区间、对称轴和对称中心;
(2)该函数图象可由
的图象经过怎样的平移和伸缩变换得到？
(1)周期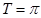
，增区间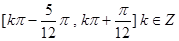
，对称轴
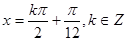对称中心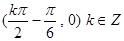
(2)见解析
解析试题分析：(1)最小正周期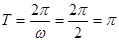
---------------------2分
令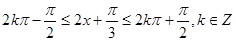
-----------------3分
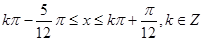------------------4分
原函数的单调增区间是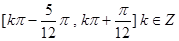 ----------5分
令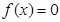
得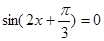
， --------------6分
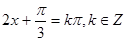，对称中心为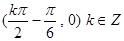 ----------7分
令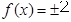
得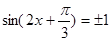
,
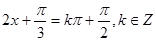, -----------8分对称轴为直线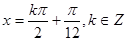 ----------------9分
(2)方法1：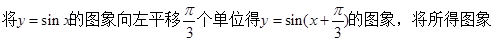
……………………………………..12分(每个变换各得1分)
方法2：
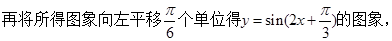
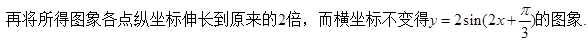………………..12分(每个变换各得1分)
考点：三角函数性质及平移伸缩变换
点评：三角函数性质中的周期性单调性对称性是常出现的考点，需熟练掌握
科目：高中数学 来源： 题型：解答题
已知函数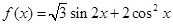
.
(Ⅰ) 当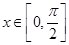
时，求函数f(x)的值域；
(Ⅱ)设a,b,c分别为△ABC三个内角A，B，C的对边，f(C)=3,c=1,ab=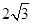
，求a,b的值。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝2sinxcosx＋cos2x(x∈R).
(1)求f(x)的最小正周期和最大值；
(2)若θ为锐角，且f(θ＋
)＝
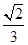，求tan2θ的值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本小题满分14分）已知向量
，
，设函数
的图象关于直线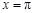
对称，其中
，
为常数，且
.
（1）求函数
的最小正周期；
（2）若
的图象经过点
，求函数在区间
上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
为第三象限角，
.
；
，求
的终边经过点
求
的值。
的图象上相邻的最高点与最低点的坐标分别为M（
，求此函数的解析式及单调递增区间。
，函数
.
的最大值与最小正周期；
成立的
的取值范围.
。
的振幅和最小正周期；
时,函数
时，求