
 中,平面
中,平面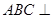 平面
平面 ,
,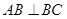 ,
,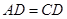 ,
,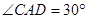 。
。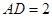 ,
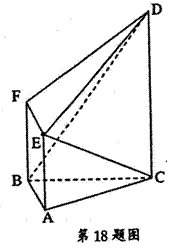
, ,求四面体
,求四面体 的体积;
的体积;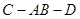 为
为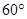 ,求异面直线
,求异面直线 与
与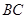 所成角的余弦值。(12分)
所成角的余弦值。(12分)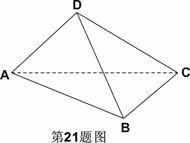
 ;(2)
;(2)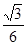 .
.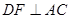 ,故由平面ABC
,故由平面ABC 平面ACD,知
平面ACD,知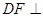 平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知
平面ABC,即DF是四面体ABCD的面ABC上的高,再利用由勾股定理易知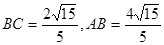 ,得到体积。
,得到体积。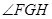 是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由
是异面直线AD与BC所成的角或补角设E为边AB的中点,则EF//BC,由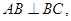 知
知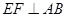 ,又由(1)有
,又由(1)有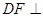 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知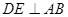 ,
,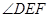 为二面角C—AB—D的平面角,由题设知
为二面角C—AB—D的平面角,由题设知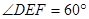 ,设AD=a,则
,设AD=a,则 ,在
,在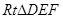 中,
中,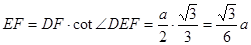
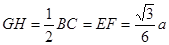 ,因为
,因为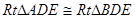 ,故
,故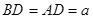 ,
, 中,
中, ,又
,又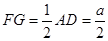 ,从而在
,从而在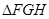 中,因
中,因 再利用余弦定理求解得到异面直线所成的角。
再利用余弦定理求解得到异面直线所成的角。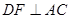 ,
, 平面ACD,知
平面ACD,知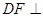 平面ABC,
平面ABC,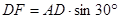 =1,……….2分,
=1,……….2分,
 ,在
,在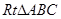 中,
中,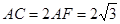 ,
, ,
,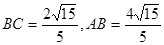 ,
,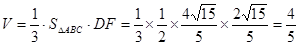 ………….4分
………….4分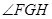 是异面直线AD与BC所成的角或补角。……….6分,
是异面直线AD与BC所成的角或补角。……….6分,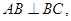 知
知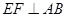 ,
,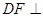 平面ABC,故由三垂线定理知
平面ABC,故由三垂线定理知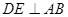 ,
,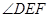 为二面角C—AB—D的平面角,
为二面角C—AB—D的平面角,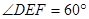 ,……….8分,
,……….8分, ,在
,在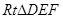 中,
中,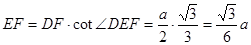 ,
,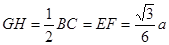 ,因为
,因为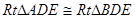 ,故
,故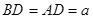 ,从而,在
,从而,在 中,
中, ,又
,又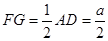 ,从而在
,从而在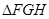 中,因
中,因 ,由余弦定理得
,由余弦定理得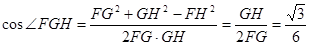 ,
,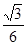 。…….12分
。…….12分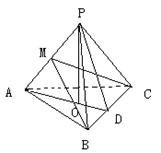


科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
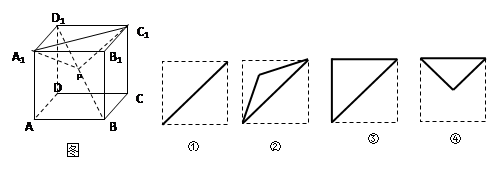
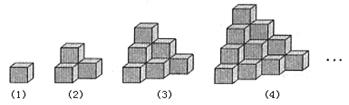
| A.以下四个图形都是正确的 | B.只有(1)(4)是正确的 |
| C.只有(1)(2)(4)是正确的 | D.只有(2)(3)是正确的 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com