
| t 小时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y 米 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
| 2π |
| T |
| 2π |
| 12 |
| π |
| 6 |
|
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 4 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
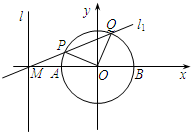 已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).
已知直线l的方程为x=-2,且直线l与x轴交于点M,圆O:x2+y2=1与x轴交于A,B两点(如图).| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、1 | ||
B、5
| ||
| C、4 | ||
D、5(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、有时可以把分类变量的不同取值用数字表示,但这时的数字除了分类以外没有其他含义 |
| B、在统计学中,独立性检验就是检验两个分类变量是否有关系的一种方法 |
| C、在进行独立性检验时,可以先利用二维条形图粗略的判断两个分类变量是否有关系 |
| D、通过二维条形图可以精确的给出所得结论的可靠程度 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 22 | 38 | 55 | 65 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com