
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| | 甲厂 | 乙厂 | 合计 |
| 优质品 | | | |
| 非优质品 | | | |
| 合 计 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
某种产品的广告费支出z与销售额y(单位:万元)之间有如下对应数据:
若广告费支出z与销售额y回归直线方程为多一6.5z+n(n∈R).
(1)试预测当广告费支出为12万元时,销售额是多少?
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
(1)若甲,乙两个小组的数学平均成绩相同,求a的值.
(2)求乙组平均成绩超过甲组平均成绩的概率.
(3)当a=2时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值为2分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有工人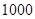 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外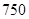 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 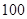 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 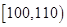 | 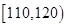 |  | 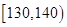 | 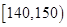 |
| 人数 | 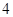 |  |  | 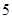 |  |
| 生产能力分组 | 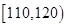 |  | 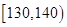 | 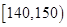 |
| 人数 |  |  |  |  |
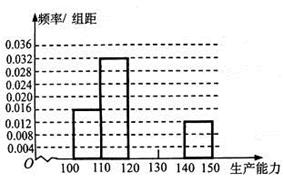
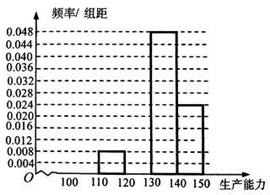
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图; 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y/μm | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到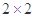 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
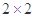 列联表;
列联表;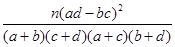
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从发生汽车碰撞事故的司机中抽取2 000名司机.根据他们的血液中是否含有酒精以及他们是否对事故负有责任.将数据整理如下:
| | 有责任 | 无责任 | 合计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1 200 |
| 合计 | 1 350 | 650 | 2 000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 =bx+a.
=bx+a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com